A triangle has corners at #(1 ,9 )#, #(5 ,7 )#, and #(3 ,8 )#. How far is the triangle's centroid from the origin?

Question

1776 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-10T07:08:23

#sqrt73# units

If,
#(x_1, y_1) => (1, 9)#
#(x_2, y_2) => (5, 7)#
#(x_3, y_3) => (3, 8)#
are the vertices of a triangle then,

Centroid (G) of a triangle is given by,
#G = ((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)#

So, substituting the above values we get,
#G = (3, 8)#

Now, to find distance 'd' between #(0, 0)# and #(3, 8)# use distance formula

#d = sqrt((8 - 0)^2 + (3 - 0)^2)#

#d = sqrt73# units

...............................................

Answer 2 · 2018-01-10T07:15:24

Distance of centroid from origin is #color(red)(8.544)#

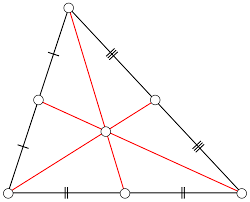
enter image source here

Formula to get centroid of a triangle, given the coordinates of three vertices is

#G (x,y) = (x1 + x2 + x3)/3, (y1 + y2 + y3)/3#

#G_x = (1 + 5 + 3) /3 = 3#

#G_y = (9 + 7 + 8) / 3 = 8#

Coordinates of centroid #G(x,y) = (3,8)#

Coordinates of origin #O(x,y) = (0.0)#

Distance of centroid from origin is
#d = sqrt((3-0)^2 + (8-0)^2) = sqrt(3^2 + 8^2) = **8.544**#