.
Point #P#, which is shown as a red dot, is at a distance #d# from the center of a circle. Below, you can see the three different possibilities for point #P#.
#(1)#, Point #P# is at a distance #d# which is smaller than the radius of the circle (#color(red)(d < r))#.
#(2)#, Point #P# is at a distance #d# equal to the radius of the circle (#color(red)(d=r))#
#(3)#, Point #P# is at a distance #d# larger than the radius of the circle (#color(red)(d > r))#
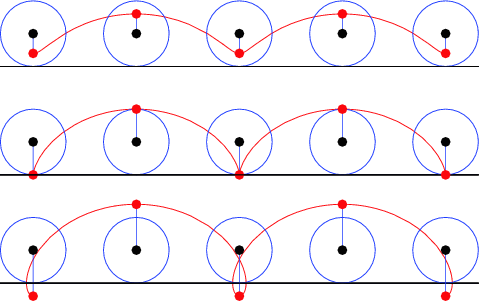
In either case, as the circle rolls along the horizontal line, Point #P# moves along the curve shown in red. That curve is called a Trochoid.
Your problem states that #color(red)(d=r)#. This special case of a trochoid is called a Cycloid and is shown below:

In the picture below, you can see Point #P# on the circumference of the circle. We will consider the horizontal line that the circle is rolling on to be the #x#-axis and the vertical line that crosses the #x#-axis at Point #O# to be the #y#-axis with Point #O# being the origin.
Initially, the circle was back where Point #P# was resting on the origin. As the circle began to roll, Point #P# moved from the origin to its currently shown location, i.e, it traveled the distance of #OP#.
Let's consider the Point #C#, the center of the circle and figure out its coordinates.
Its #x#-coordinate is #=OB# and its #y#-coordinate is #=CB#. #OB=arc PB# (both shown in yellow) since Point #P# is a fixed point on the circle and was originally where #O# is.
Therefore, if we can figure out the length of #arc PB# we will have the #x#-coordinate of #C#. #arc PB# is facing central angle #theta#. The formula for the perimeter (circumference) of a circle is:
#P=2pir# where #r# is the radius of the circle. But perimeter #P# covers #360^@# or #2pi# radians. The piece of the perimeter that would face a small angle of #1# radian would be:
#=(2pir)/(2pi)=r#
Then it would stand to reason that the piece of the perimeter facing an angle of #theta# radians would be:
#arcPB=OB=rtheta#
This means the #x#-coordinate of Point #C# is #rtheta#
The #y#-coordinate which is #CB# is #=r#
Therefore, the coordinates of Point #C# are:
#C(rtheta, r)#
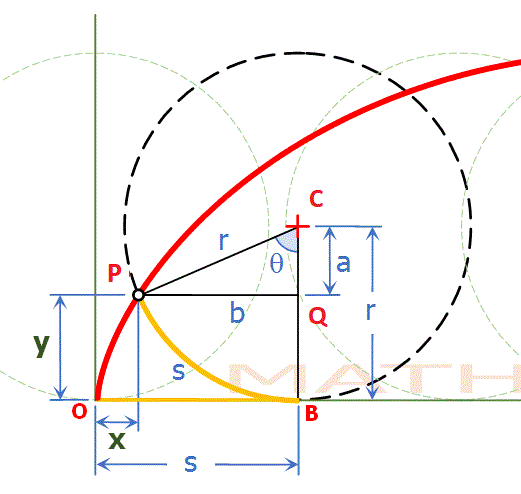
Now, let's figure out the coordinates of Point #P#.
#x=OB-PQ#
#y=CB-CQ#
Let's figure out the lengths of #PQ# and #CQ#, and substitute them in the equations of the #x# and #y# coordinates.
In triangle #Delta CPQ#,:
#sintheta=(PQ)/(PC)=(PQ)/r#
#costheta=(CQ)/(PC)=(CQ)/r#
#PQ=rsintheta#
#CQ=rcostheta#
Now, we can plug these into the coordinate equations:
#x=rtheta-rsintheta#
#y=r-rcostheta#
which is exactly what the problem wanted you to prove if you replace #d# with #r#.
To show that the formulas in the problem stand for a Trochoid regardless of whether #d# is smaller than, equal to, or larger than #r#, let's look at the picture below:
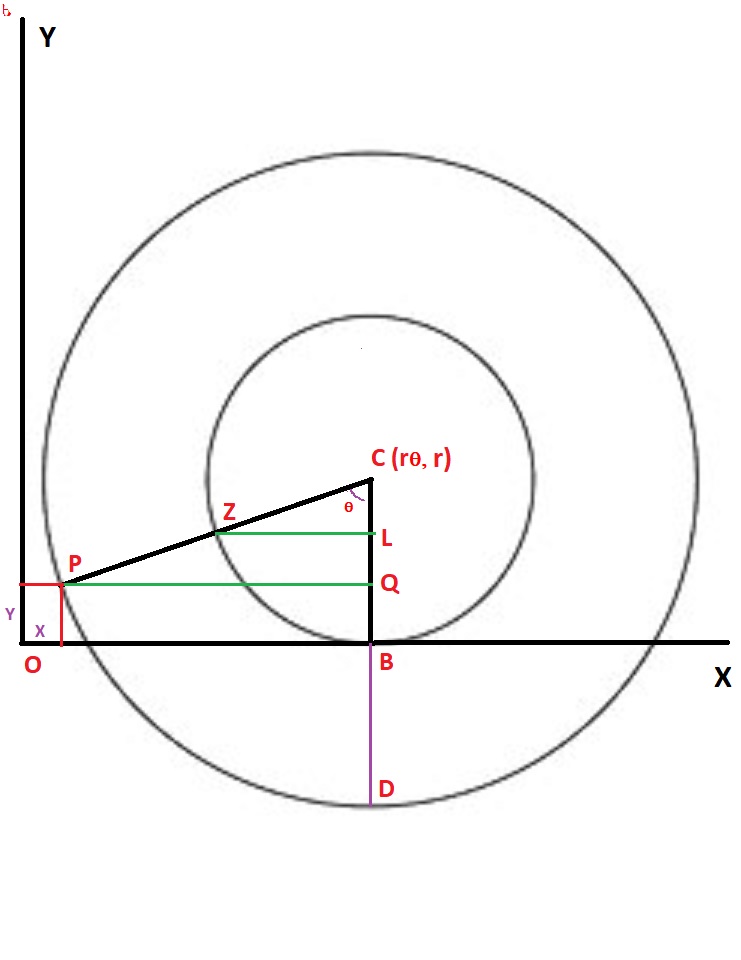
This picture shows Point #P# outside the circle. Here,
#OB=arcZB=r theta#
#CB=r#
#arcPD=d theta#
#x#-coordinate of Point #P=OB-PQ#
#y#-coordinate of Point #P=CB-CQ#
#PQ=CP sintheta=dsintheta#
#CQ=CPcostheta=dcostheta#
#x=r theta-dsintheta#
#y=r-dcostheta#
which proves the formulas given in the problem.
Similarly, if Point #P# were inside the circle. i,e #d < r#, it can be shown that the formulas hold.





