Question

What is an equation for the translation y = 4/x that has the given asymptotes. x = 4, y = -3?

Answer 1

`y=4/(x-4)-3`

Explanation:

.

If you subtract a constant from your `x` in the original function you shift the graph in the positive direction by that number of units.

And if you subtract a constant from your `y` in the original function you move its graph down by that number of units.

Your original function was `y=4/x`. When you solve for the root of the denominator, you find the vertical asymptote. In this case, it is `x=0`, i.e. the `y`-axis.

And when `x` goes to `oo`, `y=4/oo=0` which means your horizontal asymptote is `y=0`, i.e. the `x`-axis. Here is the graph:

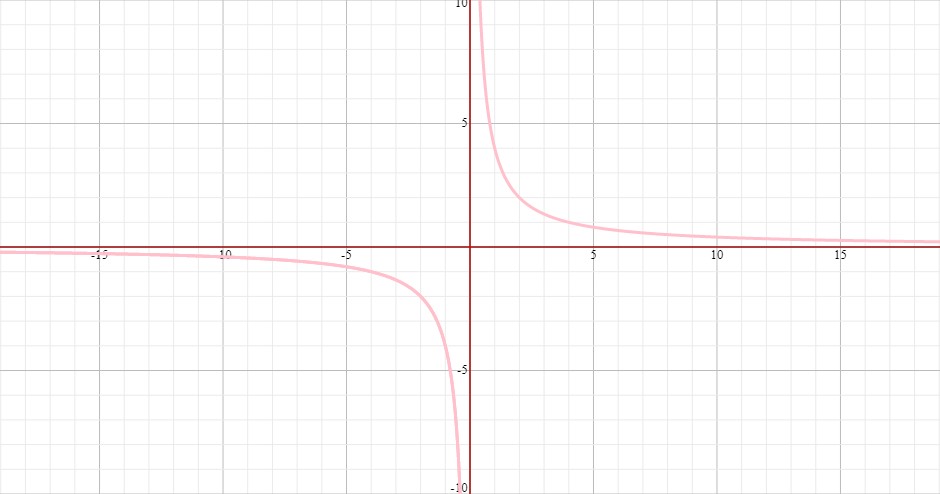
Now, you can see the transformation of `y=4/x` below. As is evident, it has shifted `4` units to the right and `3` units down with vertical asymptote at `x=4` and horizontal asymptote at `y=-3`.

Answer 2

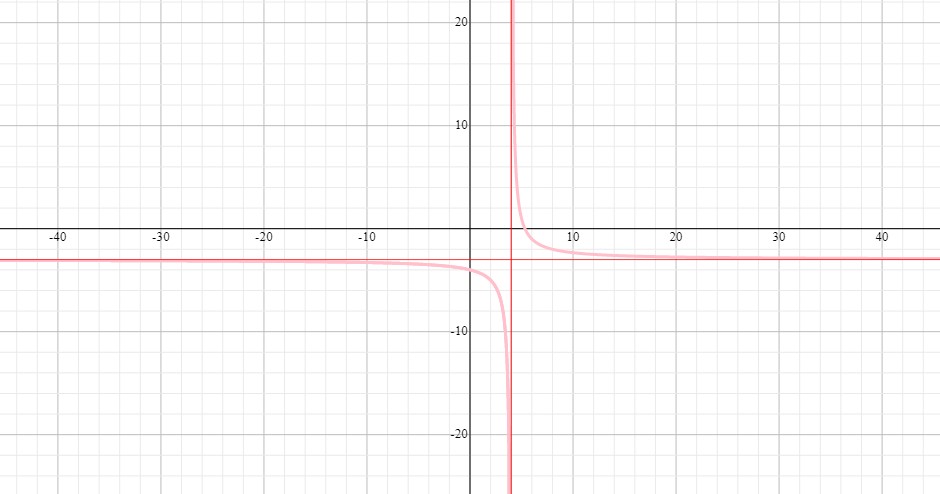
translation of 4 units right
translation of 3 units down
`y=4/(x-4)-3`

Explanation:

translation of 4 units right
translation of 3 units down

`y=f(x)->y=f(x-4)-3`
`y=4/(x-4)-3`

I hope it helps :)