I don't get my mistake on how to solve #2int (1)/(x^2-x+1)dx#, can you help me?
I got this integral:
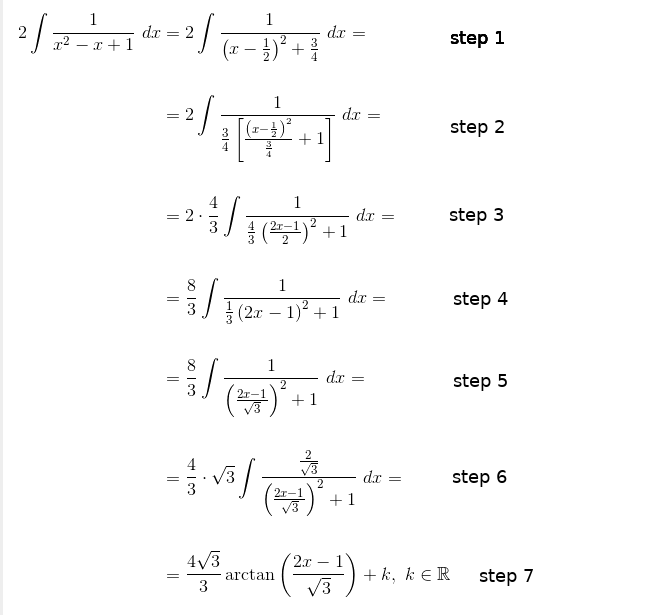
Now at the step 2 we take out #3/4# , invert it in #4/3# and multiply with #2# .
But why we don't do the same thing at the step 4?
So:
#8/3int1/(1/3(2x-1)^2+1)dx#
#3*8/3int1/((2x-1)^2+1)dx#
#8int1/((2x-1)^2+1)dx#
and so on?
I got this integral:
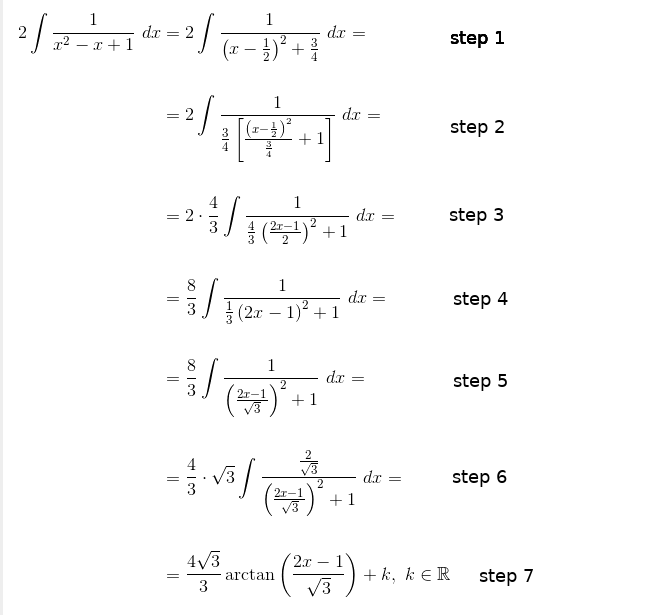
Now at the step 2 we take out
But why we don't do the same thing at the step 4?
So:
and so on?
2 Answers
Because the denominator would be
Explanation:
In order to use
Attempting to eliminate the factor
So instead, we use
There is a small arithmetic error here:
The correct working would be:
A similar error is also made in going from step 3 to step 4.
So to answer you question, to factor that
- A small recommendation:
There is a standard integral that:
Given the substitution:
you could use this to evaluate the integral from directly from step 1.


