Question

How do you find the tangent lines of parametric curves?

Show that the curve with parametric equations `x=sint`, `y=sin(t+sint)` has two tangent lines at the origin and find their equations. Illustrate by graphing the curve and its tangents.

Answer 1

`y=2x` and `y=0`

Explanation:

`x=sin(t), y=sin(t+sin(t))`

First find the derivative:

`dx/dt=cost`

`dy/dt = (1+cost)cos(t+sint)`

`dy/dx=dy/dt*dt/dx=((1+cost)cos(t+sint))/cost`

At the origin we have: `x=0` and `y=0` so from the x-coordinate:

`0=sin(t)-> t_0=0, t_1=pi`

(There are of course more values which may satisfy this but the periodicity of the sine and cosine functions means that the other solutions such as `t=2pi,4pi,...` will return the same tangent as `t=0` and `t=3pi,5pi,...` will return the same tangent as `t=pi` so we need only consider the two solutions stated).

Checking that these values of `t` satisfy `y=0`

`y=sin(0+sin(0))=0`
`y=sin(pi+sin(pi))=sin(pi+0)=0`

So `y` is also satisfied. Put these values of `t` into `dy/dx` to find the gradient of the tangent line:

For `t=0`:
`(dy/dx)_0=((1+cos(0))cos(0+sin0))/cos(0)=(2*cos(0))/cos(0)=2`

For `t=pi`

`(dy/dx)_1=((1+cos(pi))cos(pi+sinpi))/cos(pi)`

`(dy/dx)_1=((1-1)cos(pi))/cos(pi)=0`

So we have the gradients to our two tangent lines:

`m_(tan0)=2` and `m_(tan1)=0`

We also have a point at which the lines pass through, the origin: `(0,0)`

Obviously, for the equation of a straight line `y=mx+c` any line which passes through the origin will simply have `c=0.` Therefore our two tangents will be:

`y_1=2x` and `y=0`

When graphed, they look like this:

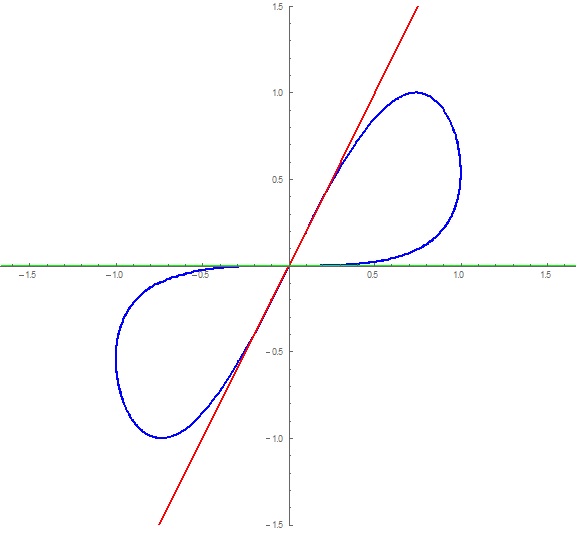
The blue line is the original parametric function and, the red line is `y=2x` and the green line (lying right on the x-axis) is `y=0`.