The tangent to y=x^2e^x at x=1 cuts the x and y-axes at A and B respectively. Find the coordinates of A and B.?
y=x^2e^x
2 Answers
See below
Explanation:
For the slope of the tangent,
the slope of the tangent at
Putting
So, the tangent passes through the point (1,e)
And, it has a slope of
So the equation of the tangent is given by,
where m is the slope.
Substituting the values,
It also passes through (1,e)
So,
therefore the equation of the tangent is,
For point A, put
Therefore point A is,
For point B, put
Therefore point B is,
A=(2/3,0) andB=(0,-2e)
Explanation:
We have a curve given by the equation:
y=x^2e^x
First we note that when
y = 1e^1 =e
So the tangent passes through
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. So if we differentiate the equation we have:
dy/dx = (x^2)(d/dxe^x) + (d/dxx^2)(e^x)
\ \ \ \ \ \ = x^2e^x + 2xe^x
\ \ \ \ \ \ = (x^2 + 2x)e^x
And so the gradient of the tangent at
m = [dy/dx]_(x=1)
\ \ = (1+2)e^1
\ \ = 3e
So, using the point/slope form
y - e = 3e(x-1)
:. y - e = 3ex-3e)
:. y = 3ex-2e
At
:. 0 = 3ex-2e => x=2/3
At
:. y = -2e
Hence the required coordinates are:
A=(2/3,0) andB=(0,-2e)
(Rounding
We can verify this solution graphically:
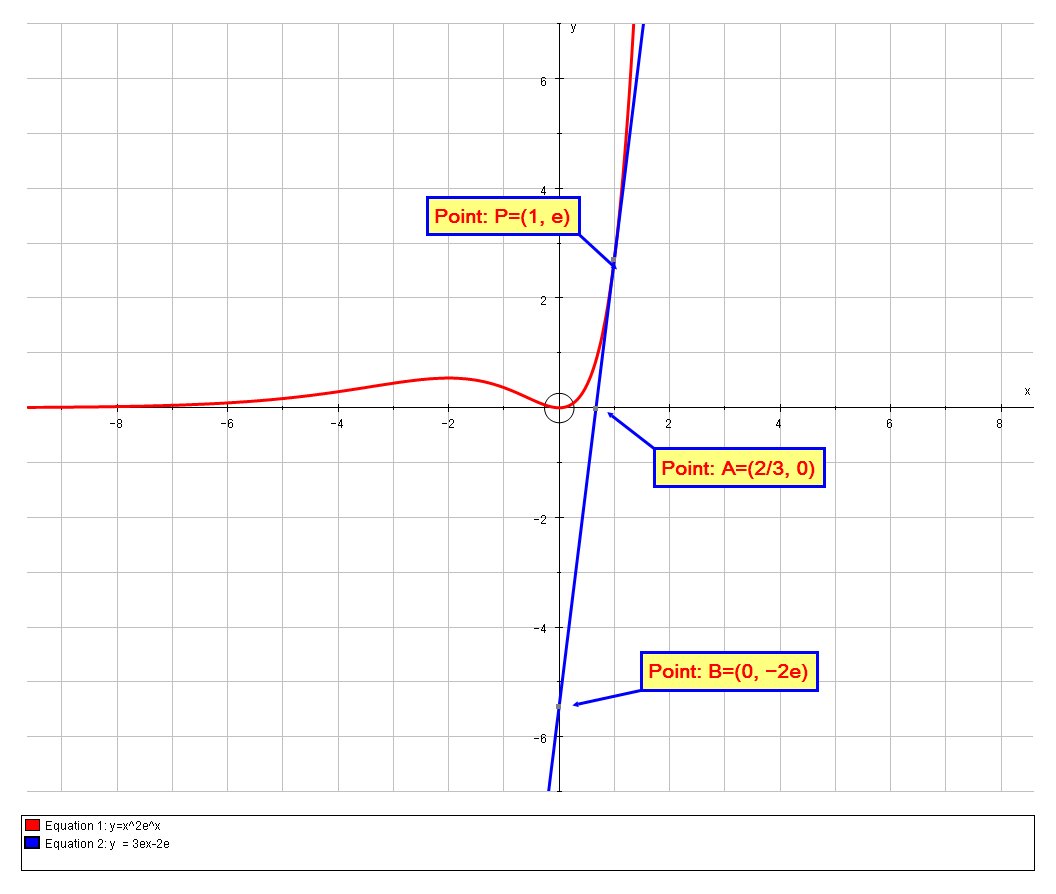 Steve M using Autograph
Steve M using Autograph