A body of 1 kg moves in a circle. At time=0 it moves with the velocity of 4 m/s and a force of 16 N is exerted on it. The force and the velocity share an angle of 60°. What is the velocity at t=1s and what is the radius of the circle?
1 Answer
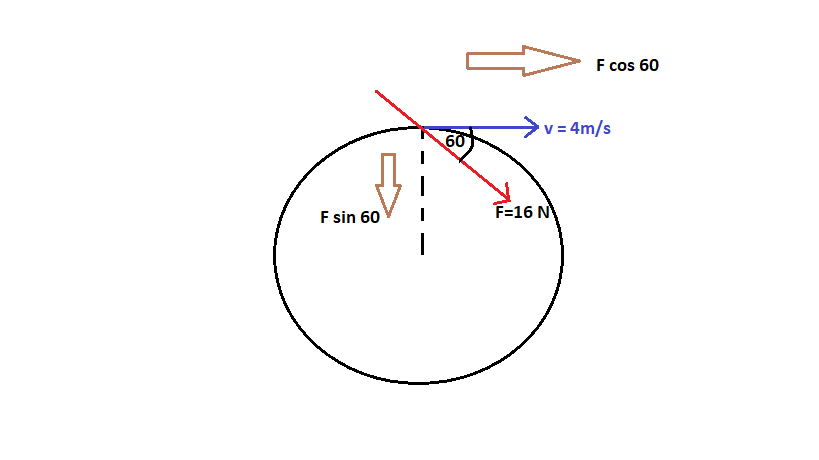
Here,the force has to be applied in the shown direction,or else the body will not be able to move in a circle,because a component of this force will tend to act centrifugally and take it away from the centre.
so,if this
So,tangential acceleration done is
so,velocity in
Now, this
so,we can write,
solving we get,

