.
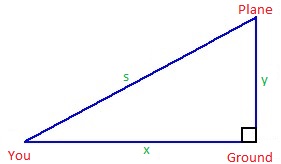
#s# is the distance between you and the plane.
#y=3# is the altitude of the plane.
#x=4# is the distance between you and the point on the ground.
The Pythagorean formula gives us:
#s^2=x^2+y^2# (#color(red)(Equation- 1)#)
We can plug the values of #x# and #y# in and find #s#
#s^2=4^2+3^2=16+9=25#
#s=5# miles
Now, we take the derivative of both sides of Equation 1with respect to time (t):
#2s((ds)/dt)=2x(dx/dt)+2y(dy/dt)#
#(ds)/dt=(2x(dx/dt)+2y(dy/dt))/(2s)=(2(x(dx/dt)+y(dy/dt)))/(2s)=#
#(cancelcolor(red)2(x(dx/dt)+y(dy/dt)))/(cancelcolor(red)2s)=#
#(ds)/dt=(x(dx/dt)+y(dy/dt))/s#
At the moment when the point on the ground is #4# miles away from you, #x# is changing at a rate of #500# miles per hour. This means:
#dx/dt=500#
Since the altitude is not changing,:
#dy/dt=0#
Now, we can plug these values in and calculate #(ds)/dt# which is the rate of change of the distance between you and the plane at that moment:
#(ds)/dt=((4)(500)+(3)(0))/5=(2000+0)/5=2000/5=400# miles per hour


