Question

A fence `8 ft` tall runs parallel to a tall building at a distance of `4 ft` from the building. What is the length of the shortest ladder that will reach from the ground over the fence to the wall of the building?

Answer 1

`16.65 \ ft\ (2 \ dp)`

Explanation:

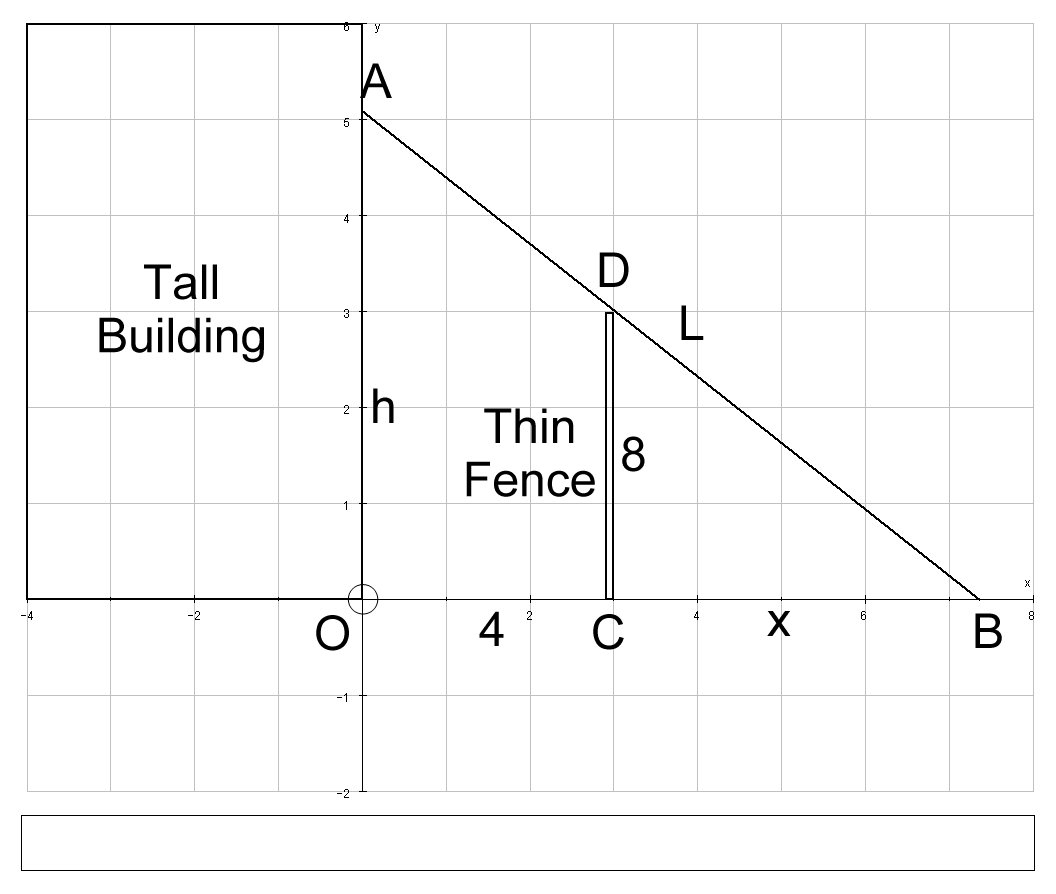
Let us set up the following variables:

# { (L, "Total length of ladder "AB, ft), (h, "Vertical height of ladder "OA, ft), (x, "Horizontal distance between ladder and fence "BC, ft) :} #

By Pythagoras, we have:

`\ \ AB^2 = OA^2 + OB^2`
`:. L^2 = h^2 + (x+4)^2` .... [A]

We also have similar triangles if we consider:

`triangle BCD` and `triangle OAB`

Which gives us the proportional relationship:

`OA:CD = OB:BC`
`:. h/8 = (4+x)/x => h = (8(4+x))/x`

Substituting this last expression for `h` into Eq [A] we get:

`L^2 = ((8(x+4))/x)^2 + (x+4)^2`
`\ \ \ \ = ((8x+32)/x)^2 + (x+4)^2`
`\ \ \ \ = (8+32/x)^2 + (x+4)^2` ... [B]

Our aim is to now minimimze `L` wrt `x`, and this involves looking for critical points of the derivative, so differentiation wrt `x` we get:

`2L (dL)/dx = 2(8+32/x)(-32/x^2) + 2(x+4)`
`\ \ \ \ \ \ \ \ \ \ = 16((x+4)/x)(-32/x^2) + 2(x+4)`
`\ \ \ \ \ \ \ \ \ \ = 2(x+4){1-256/x^3}`

At a critical point the derivative is zero and so we have the equation:

`2(x+4){1-256/x^3} = 0`

Leading to the solutions:

`x+4 = 0 => x= -4`
`1-256/x^3 = 0 => x = root(3)(256)`

We require that `x gt 0` so we discard the negative solution , leaving us with a single solution `x = root(3)(256)`

(We will omit the proof that this critical value corresponds to a minimum, we can verify this graphically, or use the second derivative test)

And so at this critical value, we can calculate the minimum ladder length using [B]:

`L^2 = (8+32/root(3)(256))^2 + (root(3)(256)+4)^2`
`\ \ \ \ = 277.1476713 ...`

`:. L = 16.6477527 .... ft`