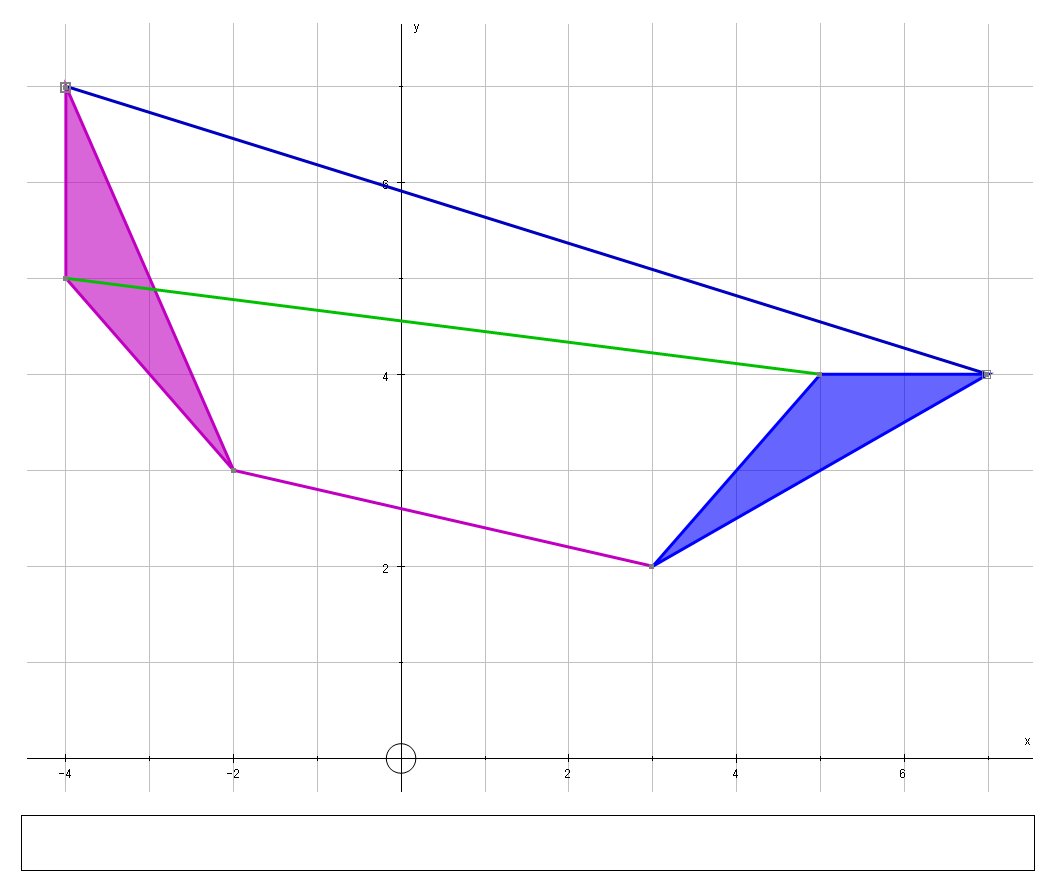
The triangle A with coordinates (3,2) (5,4) (7,4) can be mapped on to triangle D with a transformation matrix P. Find coordinates of D?
the transformation matrix for P is (""^0 ""_(1) ""^(-1) ""_(0))
the transformation matrix for P is
1 Answer
(-2,3) ,(-4,5) and(-4,7)
Explanation:
Triangle
bb ul (a)' = bb Pbb ul a ,\ \ bb ul (b)' = bb P bb ul b , and ,\ \ bb ul (c)' = bb Pbb ul c ,
Given the coordinates
bb D = ( (0,-1), (1,0)) ( (3,5,7), (2,4,4) )
\ \ \ = ( (0*3-1*2, 0*5-1*4, 0*7-1*4), (1*3+0*2, 1*5+0*4, 1*7+0*4) )
\ \ \ = ( (-2, -4, -4), (3, 5, 7) )
And so the respective coordinates of
(-2,3) ,(-4,5) and(-4,7)
And we can view the transformation graphically:
 Steve M
Steve M
We can conclude that the matrix transformation represents an anti-clockwise rotation of

