Question #ee158
1 Answer
Starting at 0, increasing the angle up to
Explanation:
This does intuitively make sense.
Nonetheless, we can also prove this using a bit of algebra and calculus. Even if you can't do the second bit, first bit should make sense. The task is:
Consider this diagram.
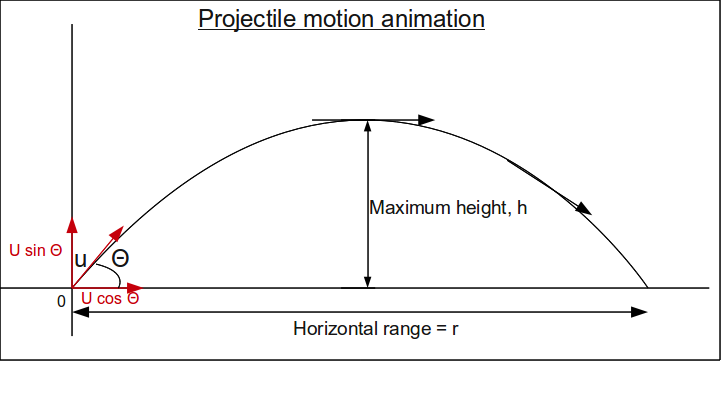 Online homework question
Online homework question
Prove that the distance
Still here? Lets go.
Let's say we are firing a projectile with a velocity of
Considering vectors, the vertical velocity of the particle is
Find the time it takes for the particle to return to the ground if we throw it up and that velocity.
Using the equation
Now, consider the horizontal motion
since
Now, as an extra challenge, can you prove that the angle that gives the maximum r is
We can use some trig identities to help us with this expression, then differentiate to find the maximum angle.
Since
Now, differentiate both sides wrt
Since
Let
We want an angle between 0 and a right angle, so we want a value in the range
