Question

If there's a 65% chance of getting diabetes and 70% chance of getting heart failure, what the probability of getting either diabetes or heart failure?

Answer 1

`179/200`

Explanation:

`65%=65/100=13/20`

Probability of getting diabetes `13/20`

`70%=70/100=1/10`

Probability of suffering heart failure `7/10`

For independent events

The probability of of event A or event B occurring is given by:

`P(AorB)=P(A)+P(B)-P(A and B)`

From our example:

Let event A be getting diabetes.

Let event B be suffering heart failure.

`P(A or B)=13/20+1/10-(13/20*7/10)=179/200`

In the above we subtracted the probability of both events occurring `P(AandB)` This is given by:

`P(AandB)=P(A)*P(B)`

The method used here may seem confusing, and is best looked at using a Venn diagram and set theory logic.

If we look at the situation we had, getting diabetes or suffering heart failure. We know that it is possible to get diabetes and suffer heart failure at the same time. This was shown as `P(AandB)`.

If we represent event A as the set A. and event B as the set B. We notice these two sets form an intersection. This is the events A and B both occurring. The intersection is expressed as `(AnnB)` which is the same as `(AandB)`.

Now if we tried to find the probability of event A or event B by just adding the two probabilities of the events together, we would find that we have also included the case of both events occurring at the same time ( the intersection ).

`(AorB)` is a union of the sets A and B, and if there is an intersection then this will also be included. This is because the intersection contains elements that belong to both A and B. Since we only require the probability of one or the other and not both, we subtract this intersection.

The Venn diagram of this would look like this.

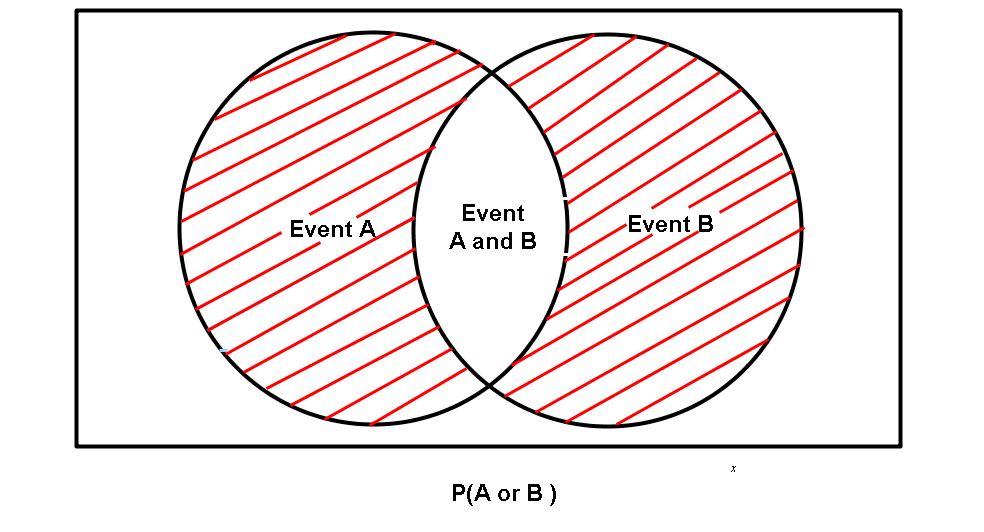
The shaded area represents the probability of event A occurring or event B occurring, but NOT both.