Question

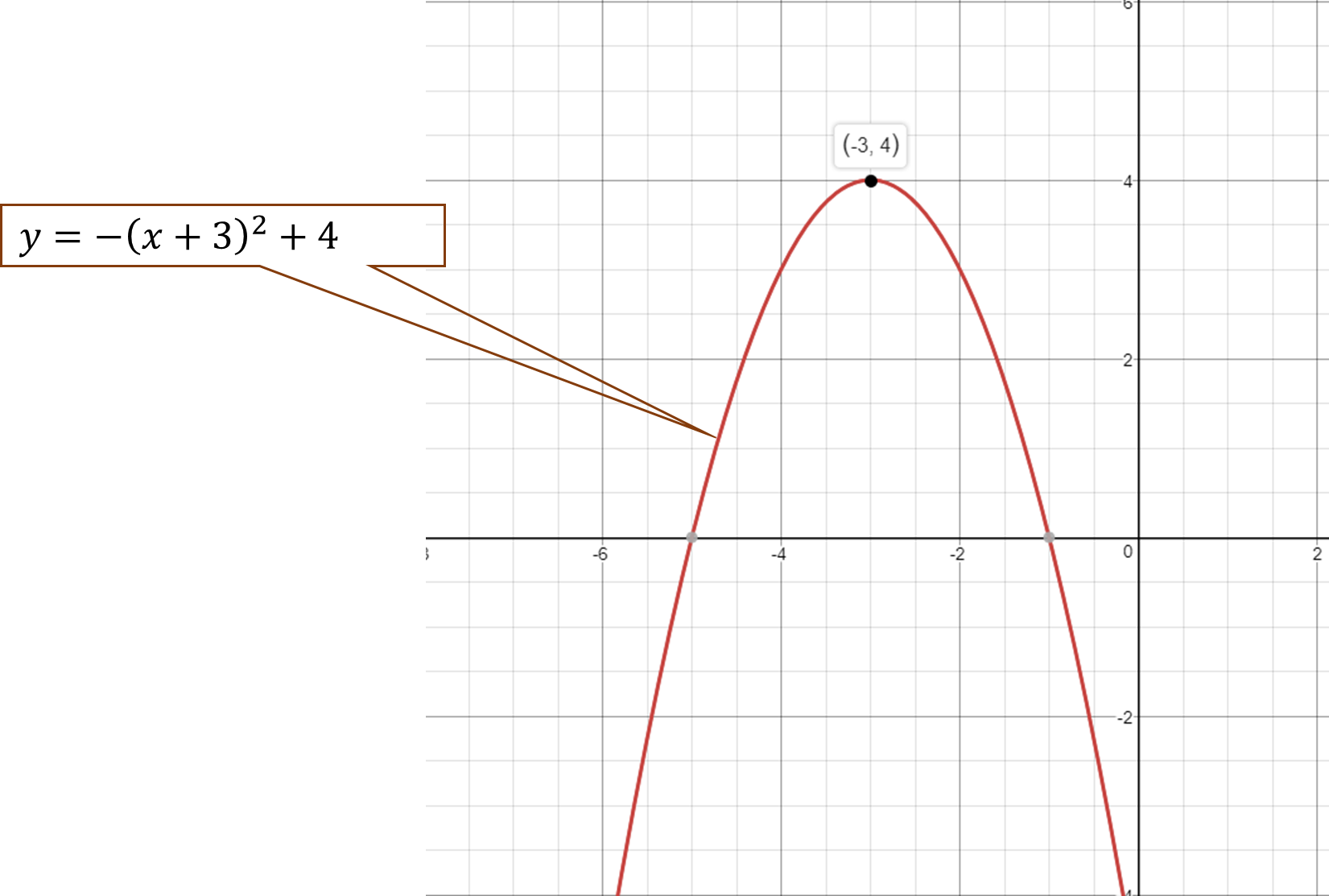
What is the maximum value of `f(x) = -(x+3)^2+4`?

Answer 1

The maximum value of `f(x)` is 4.

Explanation:

To find the maximum value of an upside-down parabola, you must find the y-coordinate of its vertex.

Since our equation is already in vertex form, we can grab the vertex pretty easily:

Vertex form: `a(x-h)^2+k`
where `(h, k)` is the parabola's vertex

`f(x)=-(x+3)^2+4`

`=-(x-(-3))^2+4`

`=> h=-3" and " k=4`

`=>"vertex" = (-3,4)`

Our maximum value, in this case, is `k`, or 4.

Answer 2

The maximum value `=4`

Explanation:

Given -

`y=-(x+3)^2+4`

`dy/dx=[[-2(x+3)]].(1)`

`dy/dx=-2x-6`

`(d^2x)/(dy^2)=-2`

`dy/dx=0=>-2x-6=0`

`x=(6)/(-2)=-3`

At `x=-3; dy/dx=0` and `(d^2y)/(dx^2)<1`

Hence the function has a maximum at `x=-3`

Maximum Value of the function.

`y=f(-3)=-(-3+3)^2+4=-(0)^2+4=4`

The maximum value `=4`