Question

A triangle has corners at `(3,7)`, `(4,1)`, and `(8,2)`. What are the endpoints and lengths of the triangle's perpendicular bisectors?

Answer 1

1. End points of the perpendiclar bisectors

`D (6,3/2), E (11/2, 9/2), F (7/2, 4)` with circum center `P (53/10, 43/10)`

1. Lengths of the perpendicular bisectors are

`PD = color(blue)(2.8862), PE = color(blue)(0.2828), PF = color(blue)(1.8248)`

Explanation:

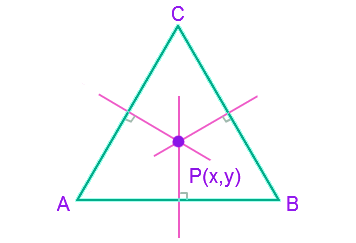
A, B, C are the vertices and Let D, E, F be the mid points of the sides a, b, c respectively.

Midpoint of BC = D = (x2 + x1)/2, (y2 + y1)/2 = (4+8)/2, (1+2)/2 =
(6,3/2)#

Slope of BC `m_(BC) = (y2-y1)/(x2-x1) = (2-1)/(8-4) = 1/4`

Slope of the perpendicular bisector through D = `-1/m_(BC) = -4`

Equation of perpendicular bisector passing through mid point D using standard form of equation `y - y1 = m * (x - x1)`

`y-(3/2) = -4 * (x - 6)`

`color(red)(2y + 8x = 51)` Eqn (D)

Similarly,

Mid point of CA = `E (11/2, 9/2)`

Slope of CA = m_(CA) = (2-7)/(8-3) = -1#

Slope of the perpendicular bisector through E = `-1/m_(CA) = 1`

Equation of perpendicular bisector passing through mid point E is

`y-(9/2) = 1 * (x - (11/2)`

`color(red)(y - x = -1)` Eqn (E)

Similarly,

Mid point of AB = `F (7/2, 4)`

Slope of AB= m_(AB) = (1-7)/(4-3) = -6#

Slope of the perpendicular bisector through F = `-1/m_(AB) = 1/6`

Equation of perpendicular bisector passing through mid point F is

`y - 4 = (1/6) * (x - (7/2)`

`12y - 48 = 2x - 7`

`color(red)(12y - 2x = 41)` Eqn (F)

Solving Eqns (D), (E), we get the coordinates of circumcenter P.

`color(green)(P (53/10, 43/10))`

This can be verified by solving Eqns (E), (F).
and the answer is `color(green)(P (53/10, 43/10)`

Length of the perpendicular bisectors PD

`PD = sqrt((6-(53/10))^2 + ((3/2) - (43/10))^2) = color(blue)(2.8862)`

Length of perpendicular bisector PE

`EP = sqrt(((11/2) - (53/10))^2 + ((9/2) - (43/10))^2) = color(blue)(0.2828)`

Length of perpendicular bisector PF
7/2, 4
`PF = sqrt(((7/2) - (53/10))^2 + (4 - (43/10))^2) = color(blue)(1.8248)`