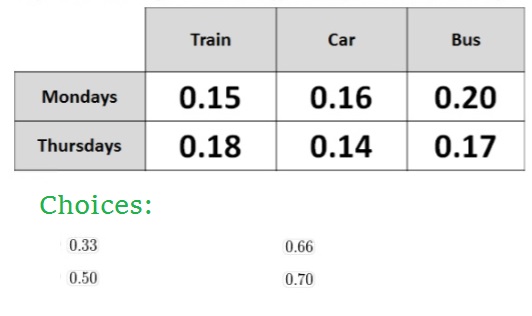
Use the table to calculate the probability that it is a Thursday, given that Jemma has travelled to work either by a train or a bus? The table show the relative frequencies with which Jemma uses each type of transport on her two travel day.
2 Answers
Explanation:
The probability is written as
To fond this probability, we find the probability that either a bus or train was taken and divide it by the probability a bus or train was taken.
Explanation:
Note that
For brevity, let us write:
{ (T = "Train"), (C = "Car"), (B = "Bus"), ("Mo" = "Monday"), ("Th" = "Thursday") :}
Then:
P("Th" | (T uu B)) = (P("Th" nn (T uu B)))/(P(T uu B))
Now:
P("Th" nn (T uu B)) = P("Th" nn T) + P("Th" nn B) = 0.18 + 0.17 = 0.35
and:
P(T uu B) = P(("Mo" uu "Th") nn (T uu B))
color(white)(P(T uu B)) = P(("Mo" nn T) uu ("Mo" nn B) uu ("Th" nn T) uu ("Th" nn B))
color(white)(P(T uu B)) = P("Mo" nn T) + P("Mo" nn B) + P("Th" nn T) + P("Th" nn B)
color(white)(P(T uu B)) = 0.15+0.20+0.18+0.17 = 0.70
So:
P("Th" | (T uu B)) = (P("Th" nn (T uu B)))/(P(T uu B)) = 0.35/0.70 = 0.50


