A triangle has corners at #(9 ,4 )#, #(3 ,9 )#, and #(5 ,8 )#. What is the area of the triangle's circumscribed circle?
1 Answer
Area of circum circle
Explanation:
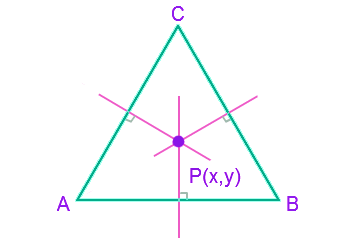
The steps to find the circum circle area of a triangle:
-
Find and Calculate the midpoint of given coordinates or midpoints (AB, AC, BC)
-
Calculate the slope of the particular line
3.By using the midpoint and the slope, find out the equation of line (y-y1) = m (x-x1)
-
Find out the other line of equation in the similar manner
-
Solve the two bisector equation by finding out the intersection point
-
Calculate the intersection point will be the circum center of the given triangle
-
Find the length of radius (r) of the circum circle, being the distance between circum center and one of the vertices.
-
Calculate the area of the circum circle using formula
#pi r^2#
Mid Point of BC
Slope of BC
Slope of PD
Equation of perpendicular bisector PD is
Mid Point of CA
Slope of CA
Slope of PE
Equation of perpendicular bisector PE is
Mid Point of AB
Slope of AB
Slope of PF
Equation of perpendicular bisector PF is
Sloving Equations (1) & (2), we get the coordinates of circum center P
Radius of circum cirlce
Verification :
Area of circum circle
