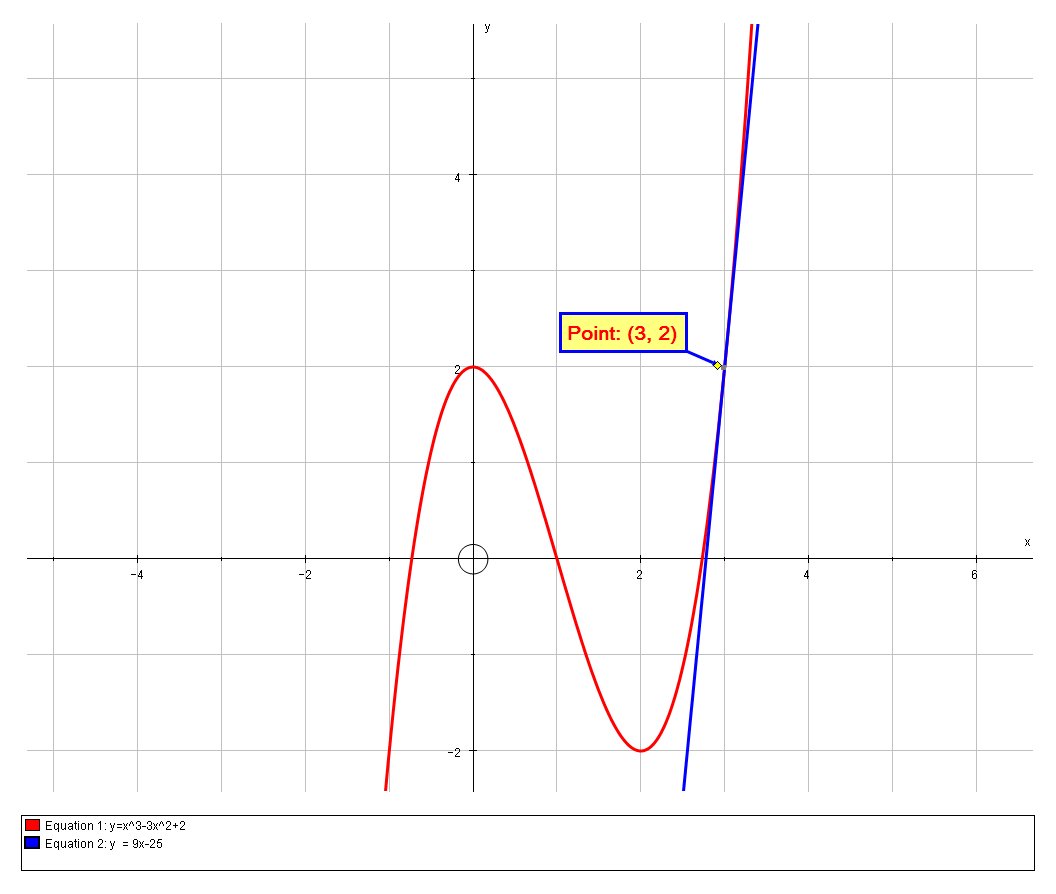
How do you find the equation of a line tangent to the function #y=x^3-3x^2+2# at (3,2)?
1 Answer
Jan 28, 2018
# y = 9x-25 #
Explanation:
We have a curve given by the equation:
# y=x^3-3x^2+2 #
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. So if we differentiate the equation we have:
# dy/dx = 3x^2-6x #
And so the gradient of the tangent at
# m = [dy/dx]_(x=3) #
# \ \ = 27-18 #
# \ \ = 9 #
So, using the point/slope form
# y - 2 = 9(x-3) #
# :. y - 2 =9x-27 #
# :. y = 9x-25 #
We can verify this solution graphically: