Question

Prove that the magnetic moment of a hydrogen atom in its ground state is eh/(4πm)?

Current, i= `e/t`
i= `e omega/(2pi)`

angular momentum, L= `(nh)/(2pi)` = mvr

Answer 1

Consider an electron in the ground state revolving around a proton in a circular orbit of radius `r` with a velocity `v`. Let its charge be represented as `-e` and its mass be `m_e`.
We know that

`v=romega`
where `omega` is the angular velocity

Current flowing due motion of electron is equal to the charge flowing through any point per second which can be found with the help of time period `T` where `omega=(2pi)/T`. This is given as

`i=-eomega/(2pi) =−(ev)/(2πr)` .......(1)

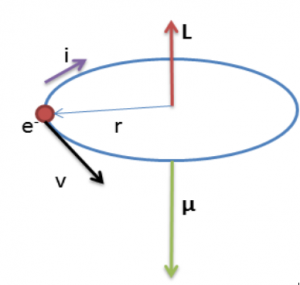
The magnetic moment `mu` due to a current loop `i` enclosing an area `A` is given by

`mu = iA`

Referring to the figure above, magnetic moment of the electron is

`mu = (−ev)/(2πr) pir^2`
`=>mu= (−erv)/2` ..........(2)

We know that angular momentum of the electron is

`vecL= vecrxx(m_evecv)`
Since radial and velocity vector are orthogonal
`:.L=rm_ev`.......(3)

Also

`L = (nh)/(2π)`

For ground state principal quantum number `n=1`

`:.L=(h)/(2π)` ......(4)

Using (3) to eliminate `rand v` from (2) we get

`mu= (−e(L/m_e))/2`
`=>mu= (−e)/(2m_e)L` ......(5)
Negative sign shows that angular momentum and magnetic moment vectors have opposite directions as shown in the figure.

Using (4) above equation can be written as

`mu= (−e)/(2m_e)((h)/(2π))`
`mu= (−eh)/(4pim_e)`