Question

What radius of a circle is required to inscribe a regular hexagon with an area of `210.44` `cm^2` and an apothem of `7.794` `cm`?

Answer 1

radius of the circumscribing circle is `color(green)(9 cm)`

Explanation:

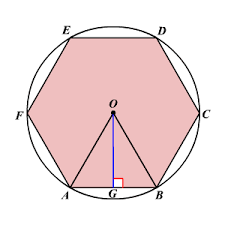
The apothem (sometimes abbreviated as apo) of a regular polygon is a line segment from the center to the midpoint of one of its sides. Equivalently, it is the line drawn from the center of the polygon that is perpendicular to one of its sides.

Given OG = 7.794 cm, `/_(AOB) = theta = 60^0` since it is a regular hexagon.

`OA = r = OG / cos (theta/2) = 7.794 / cos 30 = color(green)(9 cm`

Area of the circumscribing circle

`A_c = pi (OA)^2 = pi * 9^2 = 254.469 cm^2`

Answer 2

Radius of the circumscribing circle `color(green)(r = 9 cm)`

Explanation:

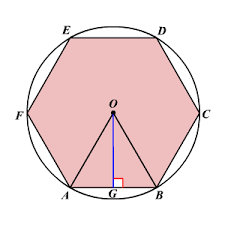
Another way of finding radius of the circum circle

Area of hexagon `A_h = 210.44 = 6 * Delta OAG`

Area of `Delta OAG = 210.44 / 6 = 35.0733 cm^2`

Since OAG an equilateral triangle,

`Delta OAG = (sqrt3/4) r^2` where r = OA = OG = AB#

`r^2 = (4/sqrt3) * 35.0733`

`color(green)(r = 9 cm)`