A triangle has corners at #(5 ,7 )#, #(2 ,1 )#, and #(1 ,6 )#. What is the area of the triangle's circumscribed circle?
2 Answers
Area of circumcircle
Explanation:
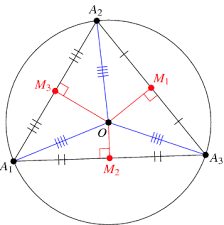
Slope of A1A2 = (7-1)/(5-2) = 2#
Slope of perpendicular bisector thro
Equation of perpendicular bisector through
Slope of A2A3 = (6-1) / (1-2) = -6#
Slope of perpendicular bisector through
Equation of perpendicular bisector through
Solving equations (1), (2) we get coordinates of circumcenter O.
Circumcircle radius
Area of circumcircle
Circumcircle area
Explanation:
I worked out the general case here .
I'm going to ignore the details of the general answer, and state the main result as: The squared radius of the circumcircle equals the product of the squared sides of the triangle divided by sixteen times the squared area of the triangle. Given triangle with sides
It's tempting to take the square root, but experience shows much smoother sailing if we don't. We can get the area from the coordinates using the Shoelace Theorem, or get
Since we need the squared sides for the numerator anyway, let's do it this way. We'll label the vertices
Circumcircle area

