What is meant by Polar Form & Rectangular form? How do we find them for Complex Equations?
1 Answer
As explained
Explanation:
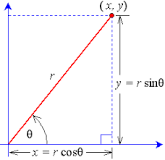
In Polar form , the length r of the vector is the absolute value or modulus of the complex number and the angle theta with the positive x-axis is the is called the direction angle or argument of
The Cartesian coordinate system in two dimensions ( also called a rectangular coordinate system or an orthogonal coordinate system ) is defined by an ordered pair of perpendicular lines (axes), a single unit of length for both axes, and an orientation for each axis.
There are two basic forms of complex number notation: polar and rectangular. Polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or modulus) and the angle of its vector (usually denoted by an angle symbol that looks like this: ∠).
The rectangular coordinates
#y = r sin theta and x = r cos theta
