A triangle has corners at #(5 ,6 )#, #(1 ,3 )#, and #(6 ,5 )#. What is the area of the triangle's circumscribed circle?
1 Answer
Area of Circumcircle
Explanation:
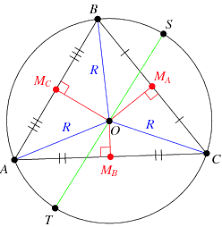
Slope of AB = (y2-y1) / (x2-x1) = (3-6) / (1-5) = 3/4#
Slope of
Cordinates of
Equation of
Slope of BC = (y2-y1) / (x2-x1) = (5-3) / (6-1) = 2/5#
Slope of
Cordinates of
Equation of
Solving Eqns (1), (2), we get circumcenter coordinates.
Radius of circumcenter R is the distance between the circumecenter O and any one of the vertices.
Area of Circumcircle
