Question

Schrodinger equation in 1 dimension Question details in the image?

In this image E = V + KE
KE = `1/2mv^2`
can you prove from this

`DeltaxDeltap >= h/(4pi)`

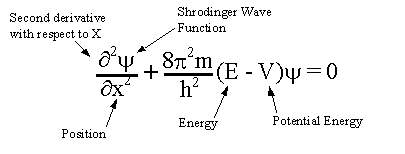
I try to solve this but instead end up proving that probablity of finding electron in all space is 1

`p^2 * ψ^2 = p^2`
This is the Schrodinger equation in 1 dimension

I'm trying to prove this from various forms of the Schrodinger equation

Answer 1

Starting from

`DeltaxDeltap_x >= ℏ"/"2`

isn't actually enlightening. In fact it adds hours of pain and suffering because you have to derive it from scratch to find the form

`DeltaxDeltap_x >= 1/2 |i << psi | [hatx"," hatp_x] | psi >> |`

where `[hatx, hatp_x] = hatxhatp_x - hatp_xhatx = iℏ`.

That would have shown that for normalized wave functions,

`DeltaxDeltap_x >= 1/2 |i cdot i ℏ |`

`>= ℏ/2 sqrt(i^"*"i)`

`>= ℏ/2`

Just know that the operators are:

`hatx = x`

`hatp_x = -iℏd/dx`

which satisfy `[hatx, hatp_x] = hatxhatp_x - hatp_xhatx = iℏ`.

This is consistent with any Schrodinger equation in one Cartesian dimension, and is easy to prove. In fact, I have done it several times, and here is one of those times.

https://socratic.org/questions/in-heisenberg-s-uncertainty-principle-is-the-uncertainty-in-the-position-a-2-dim?source=search

Here is an easy proof to go from here...

We know:

• `p = mv`
• `K = 1/2mv^2`

Thus,

`hatK = hatp^2/(2m) = (-iℏ)^2 /(2m) del^2/(delx^2) = -ℏ^2/(2m) (del^2)/(delx^2)`

So for any Schrodinger equation in one Cartesian dimension...

`hatH psi = Epsi`

`= (hatK + hatV)psi`

`= (-ℏ^2/(2m) (del^2)/(delx^2) + hatV)psi`

Thus,

`-ℏ^2/(2m) (del^2psi)/(delx^2) + hatVpsi = Epsi`

`(del^2psi)/(delx^2) - (2m)/(ℏ^2)[hatV-E]psi = 0`

`(del^2psi)/(delx^2) + (2m)/(ℏ^2)[E-hatV]psi = 0`

`color(blue)((del^2psi)/(delx^2) + (8pi^2m)/(h^2)[E-hatV]psi = 0)`

This of course does NOT tell us what the potential is. That's your responsibility to tell us.