Two forces of 125 Newton’s and 215 Newton’s act on an object, as shown in the diagram. Calculate the magnitude and direction (including a specific angle θ) of the resultant force and the equilibrant force? THE DIAGRAM IN THE DETAILS
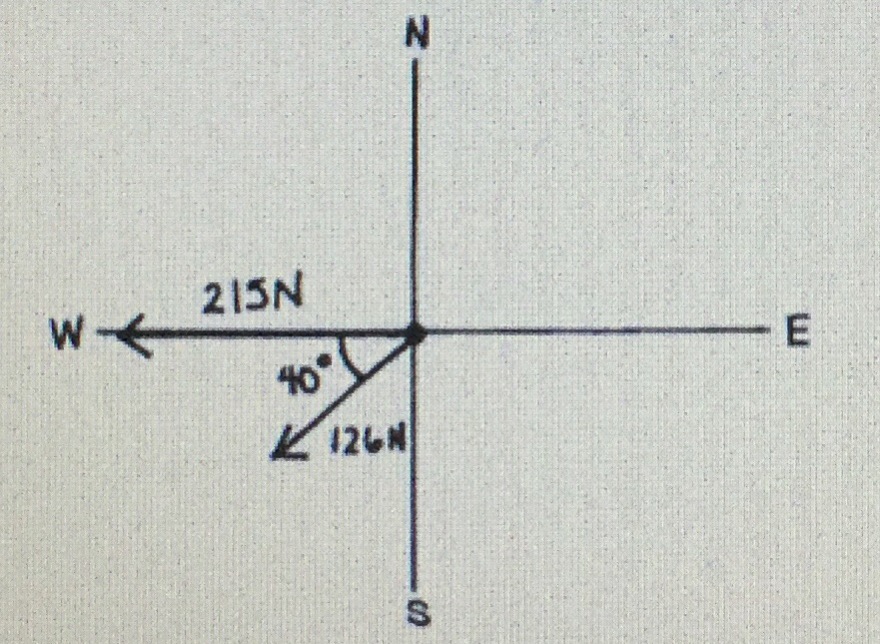
1 Answer
The resultant force is
The equilibrant is
Explanation:
This problem requires that we resolve the force vectors into
Once this is done, we can add the components easily, as the one 2-dimensional problem will be two 1-dimensional problems.
Finally, we will convert the resultant force into standard form and find the equilibrant.
Resolve into components:
Note the change of the angle used to give the direction of
Now, we add the components:
Technically, this is the resultant force. However, it should be changed back into standard form. Here's how:
However, this angle cannot be correct! It does not lie between the two vectors shown! The problem is that the argument in the
The angle we want is in the third quadrant (where tan is also positive!). So, we must subtract 180° from the above angle to get the true direction of the resultant, namely -165.4°.
A careful diagram will help you to avoid this problem!
So, our resultant force is
The equilibrant is the force that would add to this resultant and create a total of zero (that is, it balances the resultant force). This must be a vector with the same magnitude, but in the opposite direction, namely

