A boat is sailing due east parallel to the shoreline at speed of 10 miles per hour. At a given time, the bearing to a lighthouse is S 72° E, and 15 minutes later the bearing is S 66°. How do you find the distance from the boat to the lighthouse?
1 Answer
Preliminary Calculations
Explanation:
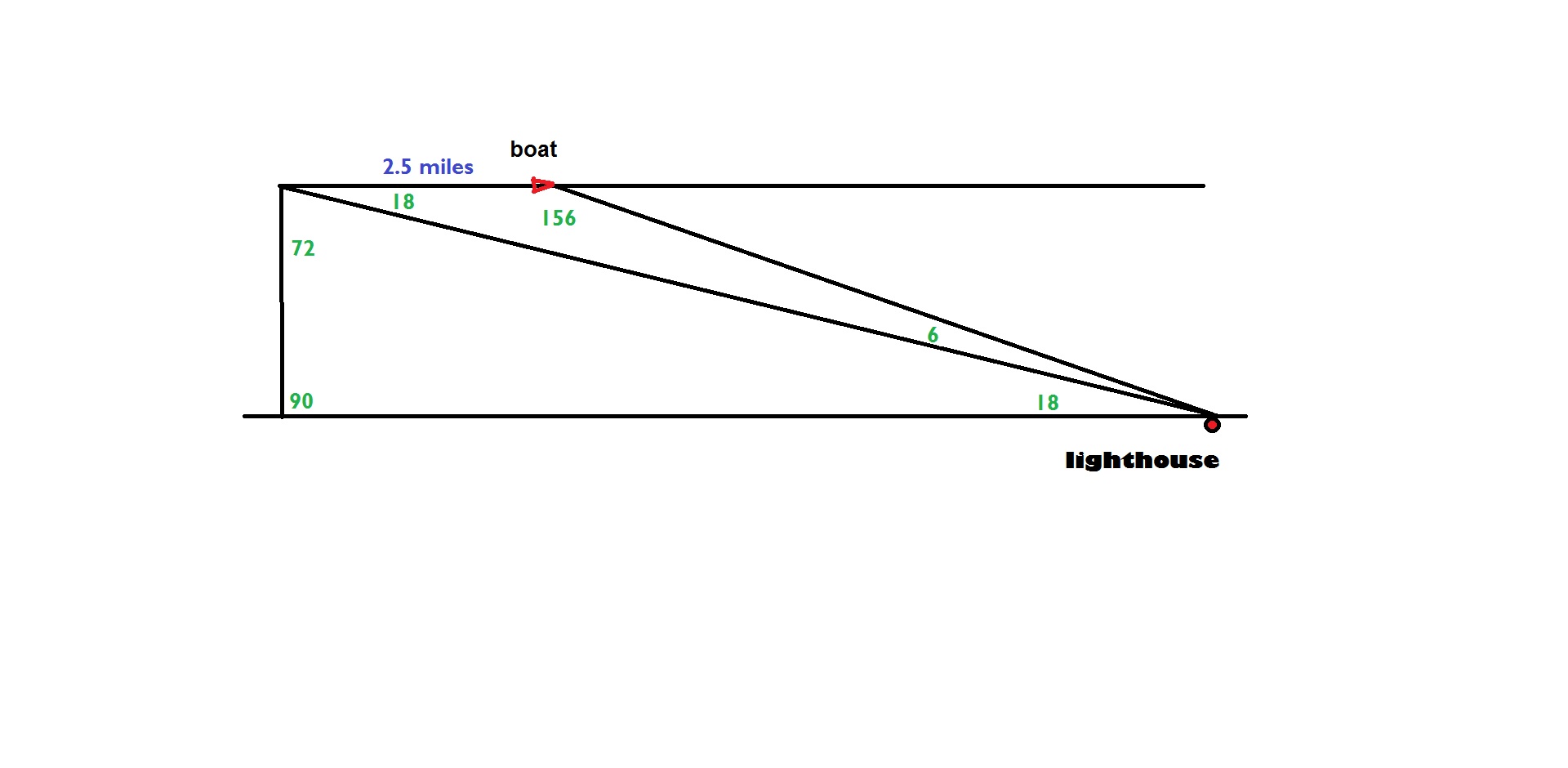
Since the boat is traveling at a rate of 10 miles per hour (60 minutes), that same boat travels 2.5 miles in 15 minutes.
Draw a diagram. [On the diagram shown, all angles are in degrees.] This diagram should show two triangles -- one with a
The angle immediately under the boat's present location measures
For the angle with the smallest measure in the diagram, I have used the fact that
This gives us an oblique triangle whose angles measure
You may now use the Law of Sines to find the direct distance to the lighthouse.
This gives a direct distance of approximately 7.4 miles.
If you want the perpendicular distance to the shore, you may now use basic trigonometry. If y is the perpendicular distance, then
This is approximately 2.9 miles.