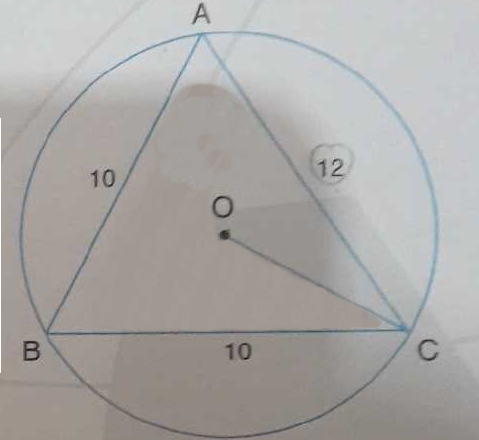
|AB|=|BC|=10\ cm , |AC|=12\ cm \Rightarrow r=?
2 Answers
Explanation:
In a triangle, there are
The circumcircle always passes through all three vertices of a triangle. Its center is at the point where all the perpendicular bisectors of the triangle's sides meet. This center is called the circumcenter.
At circumcenter, all three vertices of the circle are the same distance away from the circumcenter. Thus, the circumcenter is the point that forms the origin of a circle in which all three vertices of the triangle lie on the circle. Thus, the radius of the circumcircle is the distance between the circumcenter and any of the triangle's three vertices. It is found by finding the midpoint of each leg of the triangle and constructing a line perpendicular to that leg at its midpoint.
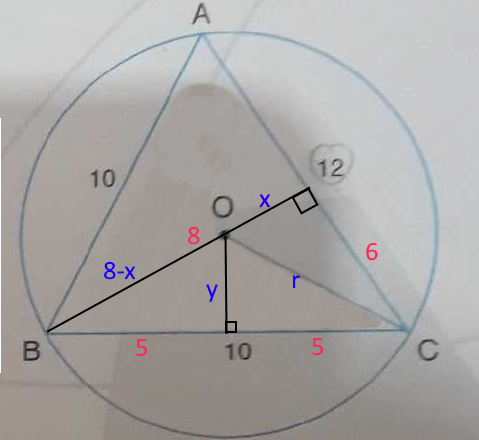
Let's say
By using pythagorean thoerem for
Let's say
For the
By putting the value of
For the
Compare the [i] and [ii], to get:
Solve to get:
Put back in [ii] to get:
Simplify:
radius of circumcircle
Explanation:
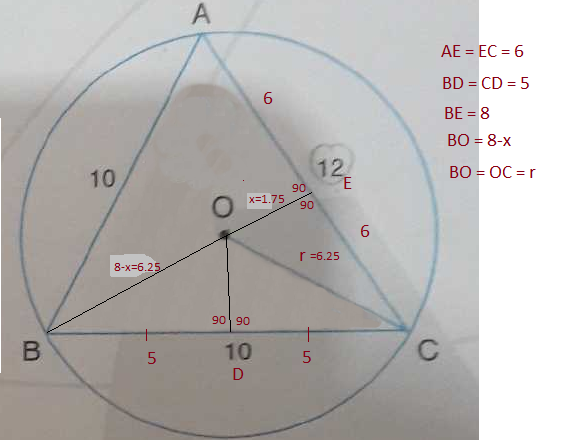
ABC is an isosceles triangle with AB = BC = 10, AC = 12
Construction : Draw perpendicular bisector from B to AC cutting at E.. Draw OD perpendicular bisector toBc.
In right triangle BEC,
Let OE = x. OB = OC = 8-x as triangle OBC is isosceles.
Consider right triangle OEC

