Question

Question #ba71a

Answer 1

Rolle's Theorem is satisfied as there are two points at

`color(blue)(x=1.868517," " x = -0.53518`

where `color(green)(f'(x) = 0`

Explanation:

Rolle's Theorem states that under certain conditions an extreme value is guaranteed to lie in the interior of the closed interval.

Rolle's Theorem

Conditions:

1. The function `color(blue)(f(x)` must be continuous on the closed interval [a, b].

2. The function f(x) must be differentiable on the open interval (a, b).

3. f(a) = f(b)

If these three conditions are satisfied then there is at least one number in the open interval (a, b) such that the derivative of f(x) is zero.

Given:

`color(brown)(f(x) = x^3-2x^2-3x`

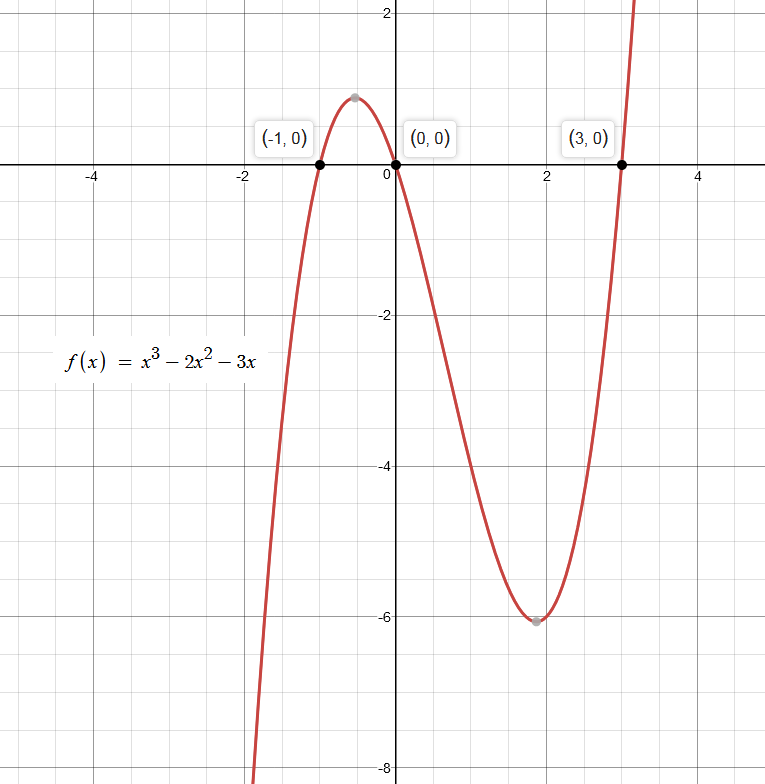
Observe that `color(brown)(f(x) = x^3-2x^2-3x` is a Cubic Function.

We will now find the x-intercepts of `f(x)`

`color(green)(f(x) = x^3-2x^2-3x`

and show that

`f'(x) = 0` at some points between the x-intercepts

We have

`f(x) = x^3-2x^2-3x`

`f(x) = x(x^2-2x-3)`

We can write this expression as

`f(x) = x(x^2+x-3x-3)`

`f(x) = x[x(x+1)-3(x+1)]`

`rArr x*(x+1)*(x-3)`

Hence the solutions to our Cubic Function are

`color(blue)(x=0; x= (-1); x= 3`

Please refer to the image of the graph below that visually presents our findings.

Next

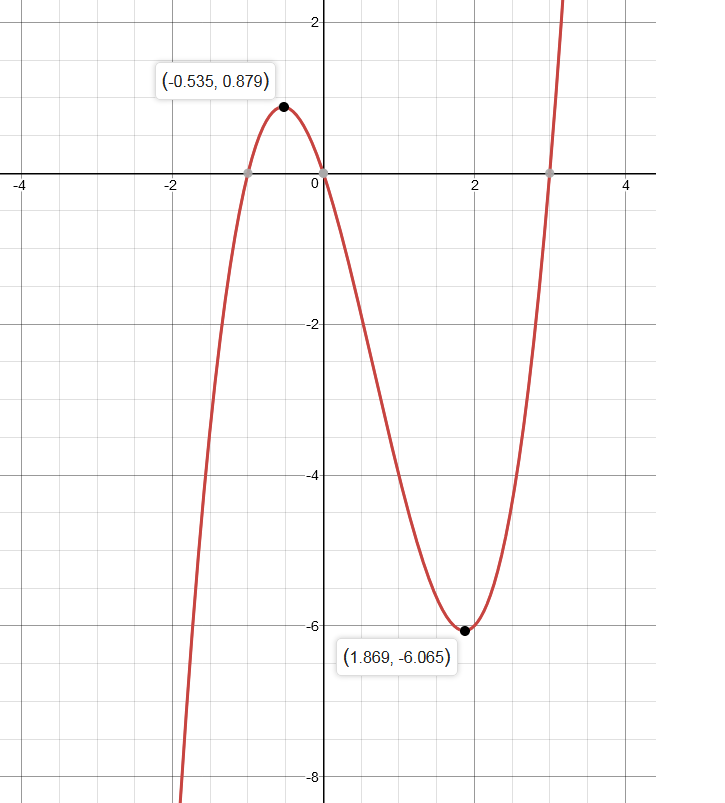
we will differentiate `color(green)(f(x) = x^3-2x^2-3x`

We will find

`d/dx [x^3 - 2x^2 - 3x]`

`rArr 3x^2-4x-3`

`:. f'(x) = 3x^2-4x-3`

Next

we will set `color(brown)(f'(x) = 0`

i.e., `3x^2-4x-3 = 0`

This is a quadratic equation

General Form of a quadratic equation is

`color(red)(ax^2+bx+c=0`

Consider our quadratic equation

`3x^2-4x-3 = 0`

Note that

`color(blue)(a=3; b=(-4) and c=(-3)`

We will use the following quadratic formula to simplify:

`x=[ -b +- sqrt(b^2 - 4ac)]/(2a)`

`x=[ -(-4) +- sqrt((-4)^2 - 4*3*(-3))]/(2*3)`

`x=[4+-sqrt(52)]/6`

Hence our roots are

`x=(2/3)+(1/3)*sqrt(13) " "(or)" "`

`x = (2/3)+(-1/3)*sqrt(13)`

`color(blue)(rArr x = 1.868517 or x = - 0.53518`

Rolle's Theorem is satisfied as there are two points at

`color(blue)(x=1.868517," " x = -0.53518`

where `color(green)(f'(x) = 0`

Please refer to the image of the graph below that visually presents our findings.