Question

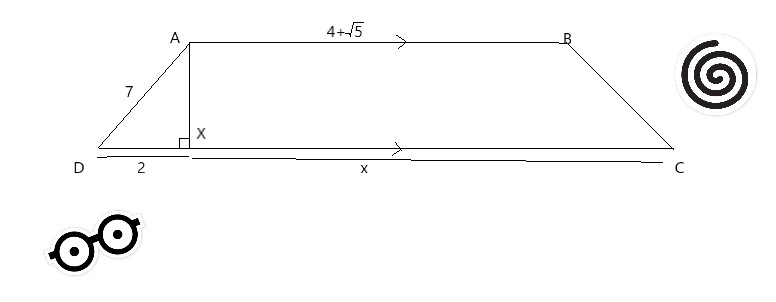
The diagram shows a trapezium ABCD in which AD=7cm and `AB=(4+sqrt5)cm`. AX is perpendicular to DC with DX=2cm and XC= x cm. Given that the area of trapezium ABCD is `15(sqrt5+2)cm^2`, obtain an expression for x in the form of `a+bsqrt5`.?

where a and b are integers

Answer 1

The answer is `=4+3sqrt5`

Explanation:

The area of a trapezium is

`"Area"=1/2*(AB+DC)*AX`

`AB=4+sqrt5`

`DC=2+x`

Apply Pythagoras theorem

`AX=sqrt(AD^2-DX^2)=sqrt(7^2-2^2)=sqrt(49-4)=sqrt45=3sqrt5`

The `"Area" = 15(sqrt5+2)`

Therefore,

`1/2*(4+sqrt5+2+x)*3sqrt5=15(sqrt5+2)`

`(6+sqrt5+x)3sqrt5=30(sqrt5+2)`

`x+6+sqrt5=30(sqrt5+2)/(3sqrt5)=10(1+2/5sqrt5)`

`x=10+20/5*sqrt5-6-sqrt5`

`=4+3sqrt5`