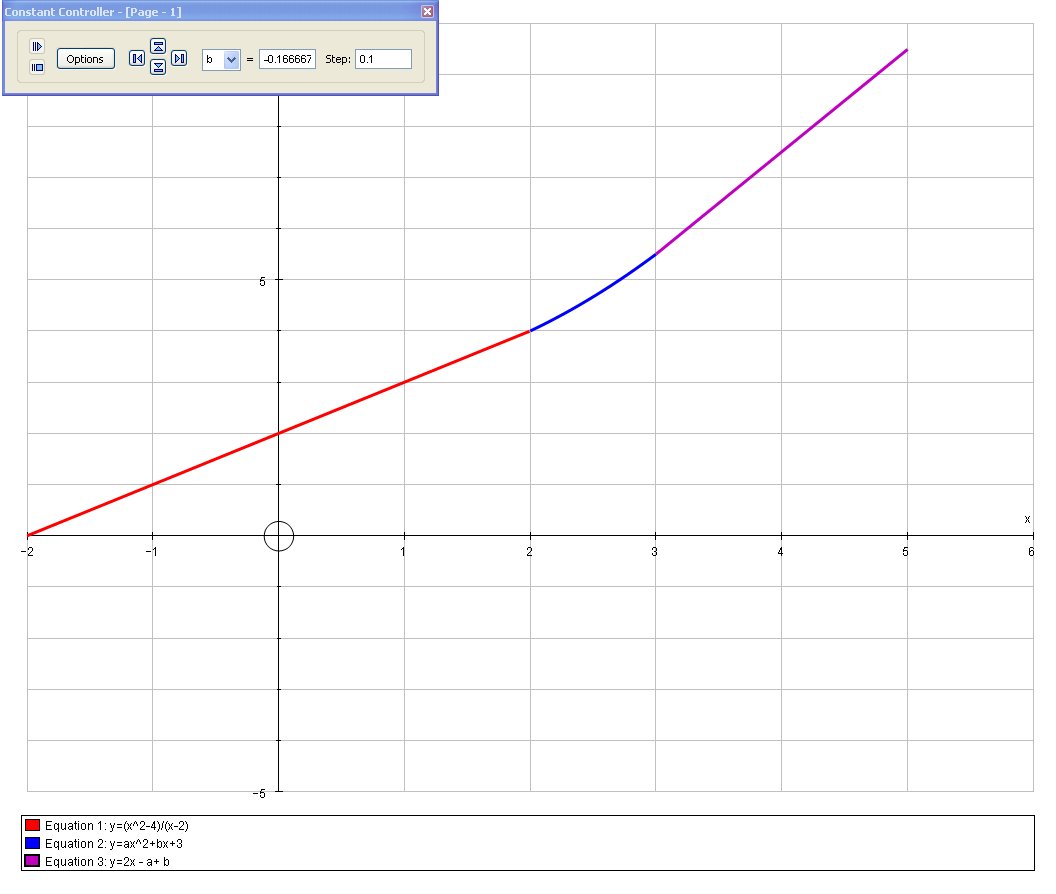
What are the values for a & b that make f continuous? f(x)=(x^2-4)/(x-2) if x<=2; f(x)=ax^2+bx+3 if 2<x<3; f(x)=2x-a+b if x>=3
1 Answer
a = 1/3 \ \ \ , andb = -1/6
Explanation:
We have:
f(x)={ ((x^2-4)/(x-2), x le 2), (ax^2+bx+3, 2 < x < 3), (2x - a+ b, x ge 3) :}
The issue of continuity will be focused on the intersection points between the various function definitions. i.e.
Using the appropriate definition of
f(x) = (x^2-4)/(x-2)
We note that when
f(2) = lim_(x rarr 2) (x^2-4)/(x-2)
\ \ \ \ \ \ \ = lim_(x rarr 2) ((x+2)(x-2))/(x-2)
\ \ \ \ \ \ \ = lim_(x rarr 2) (x+2)
\ \ \ \ \ \ \ = 4
In order to ensure continuity at
lim_(x rarr 2^-) (x^2-4)/(x-2) = lim_(x rarr 2^+) ax^2+bx+3
:. 4 = 4a+2b+3
:. 4a+2b = 1 ..... [A]
Using the appropriate definition of
f(x) = 2x - a+ b
And so we have:
f(3) = 6-a+b
In order to ensure continuity at
lim_(x rarr 3^-) ax^2+bx+3 = lim_(x rarr 3^+) 2x - a+ b
:. 9a+3b+3 = 6 - a+ b
:. 10a+2b = 3 ..... [B]
We now have two equations, [A] and [B] in two unknowns
a = 1/3 \ \ \ , andb = -1/6
And we can verify the solution graphically: