This problem includes factorial. Can anybody solve this?
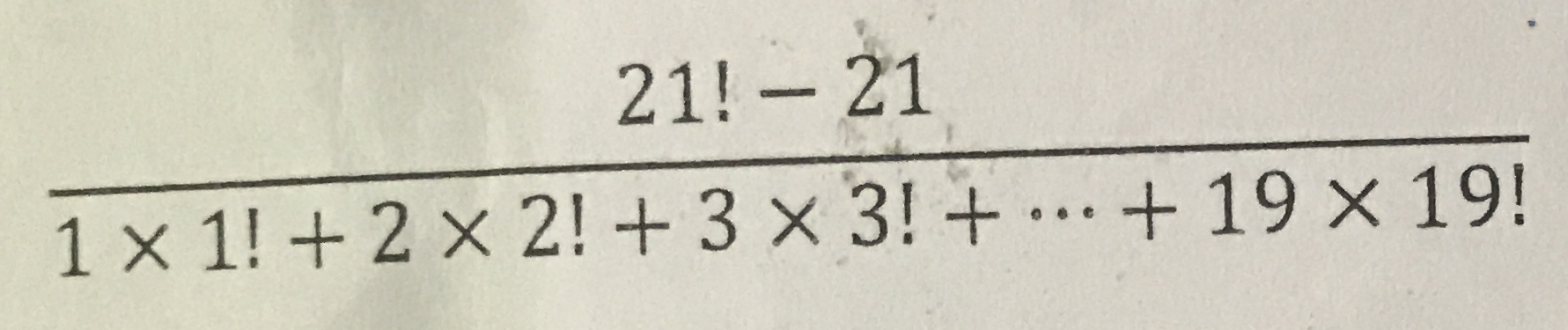
1 Answer
Explanation:
Let us look at the first few sums of the form:
1 xx 1! + 2 xx 2! + ... + n xx n!
We find:
1 xx 1! = 1
1 xx 1! + 2 xx 2! = 5
1 xx 1! + 2 xx 2! + 3 xx 3! = 23
1 xx 1! + 2 xx 2! + 3 xx 3! + 4 xx 4! = 119
Compare
It looks like:
1 xx 1! + 2 xx 2! + ... + n xx n! = (n+1)! - 1
Can we prove it?
Let
1 xx 1! + 2 xx 2! + ... + n xx n! = (n+1)! - 1
We find:
1 xx 1! = 1 = 2! - 1 = (1+1)! - 1
So
Suppose
Then:
1 xx 1! + 2 xx 2! + ... + n xx n! + (n+1) xx (n+1)!
= (n+1)! - 1 + (n+1) xx (n+1)!
= (1+(n+1)) (n+1)! - 1
= ((n+1)+1)! - 1
That is, if
So by induction
Then:
(21! - 21)/(1 xx 1! + 2 xx 2! + ... + 19 xx 19!)= (21 xx (20 !- 1))/(20! - 1) = 21
Remarks
Oliver Heaviside famously said "Mathematics is an experimental science, and definitions do not come first, but later on."
Note that I have not used a pat formula for the identity of factorial sum and factorial above. Instead, I tried a few values, noticed a pattern and then proved the formula.
I would recommend that you do not memorise a whole number of identities by heart. There are a few that are really useful, but in general you should be able to derive any that you need.

