-2x^2+8x -6:−2x2+8x−6:
factorise:
-2(x^2-4x+3)−2(x2−4x+3)
(-4)/2 = -2−42=−2
x^2-4x + 4 = (x-2)^2x2−4x+4=(x−2)2
x^2 - 4x + 3 = (x-2)^2 - 1x2−4x+3=(x−2)2−1
-2(x^2-4x+3) = -2((x-2)^2-1)−2(x2−4x+3)=−2((x−2)2−1)
=-2(x-2)^2 + 2=−2(x−2)2+2
a(x-h)^2 + k = -2(x-2)^2 + 2a(x−h)2+k=−2(x−2)2+2
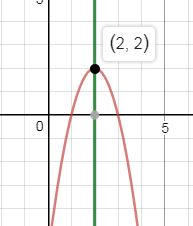
turning point: (-h,k)(−h,k), where x=hx=h is the axis of symmetry.
(-h, k) = (2,2)(−h,k)=(2,2)
x= 2x=2 is the axis of symmetry.
since the coefficient of x^2x2 is negative (-2)(−2), the graph opens to the bottom.
the point (-h, k)(−h,k) is therefore a maximum point.
since the maximum point is the highest possible, the range is equal to or below 22.
{y: y<=2}{y:y≤2}
 desmos.com/calculator
desmos.com/calculator
6x^2+3x-18:6x2+3x−18:
factorised:
6(x^2+0.5x-3)6(x2+0.5x−3)
x^2+0.5x+0.0625 = (x+0.25)^2x2+0.5x+0.0625=(x+0.25)2
x^2+0.5x-3 = (x+0.25)^2-3.0625x2+0.5x−3=(x+0.25)2−3.0625
6((x+0.25^2)-3.0625) = 6(x+0.25^2) - 18.3756((x+0.252)−3.0625)=6(x+0.252)−18.375
a(x-h)^2 + k = 6(x+0.25)^2 - 18.375a(x−h)2+k=6(x+0.25)2−18.375
turning point: (-h,k)(−h,k), where x=-hx=−h is the axis of symmetry.
(-h, k) = (-0.25,-18.375)(−h,k)=(−0.25,−18.375)
x= -0.25x=−0.25 is the axis of symmetry.
since the coefficient of x^2x2 is positive (6)(6), the graph opens to the top.
(-h, k)(−h,k), therefore, is a minimum point.
(-h, k) = (-0.25, -18.375)(−h,k)=(−0.25,−18.375)
since the minimum point is the lowest possible, the range is equal to or above -18.375−18.375.
{y:y>=-18.375}{y:y≥−18.375}
 desmos.com/calculator
desmos.com/calculator


desmos.com/calculator
desmos.com/calculator

