As we know given
#f(x,y)=x^3 - x y^2 + y^3 - 1=0# we have
#(dy)/(dx) = - (f_x)/(f_y) = (y^2-3x^2)/(3y^2-2x y)#
with the companion condition #f(x,y)=0#
Now if we need to compute the coordinates for which #(dy)/(dx) = 0# in the first quadrant, we should solve
#{(x^3 - x y^2 + y^3 - 1=0),(y^2-3x^2=0):}#
obtaining the real solutions
#(-0.517964,0.897141)# and #(0.678877, 1.17585)#
so the solution is for
#(x,y)=(0.678877, 1.17585)#
Attached the plot for #f(x,y)=0# in blue and the point found in red.
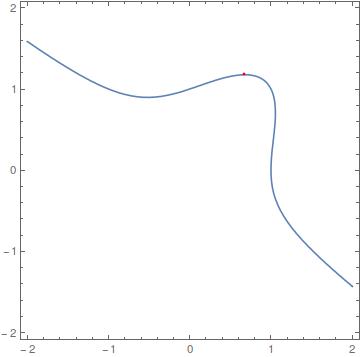
NOTE
To solve the system
#{(x^3 - x y^2 + y^3 - 1=0),(y^2-3x^2=0):}#
making #y = lambda x# we have
#{(x^3(1-lambda^2+lambda^3)=1),(lambda^2=3):}#
giving after some considerations
#lambda = sqrt3# and #x = (2/23 + (3 sqrt[3])/23)^(1/3)#
and consequently
#y = sqrt[3] (2/23 + (3 sqrt[3])/23)^(1/3)#


