Question

Related Rates?

A road running north to south crosses a road going east to west at the point P. Car A is driving north along the first road, and an airplane is flying east above the second road. At a particular time the car is 15 kilometers to the north of P and traveling at 60 km/hr, while the airplane is flying at speed 190 km/hr 10 kilometers east of P at an altitude of 2 km. How fast is the distance between the car and the airplane changing?

Answer 1

`154.37` `Km`/`hr`

Explanation:

.

The picture below depicts the the locations of the Car and the Airplane.

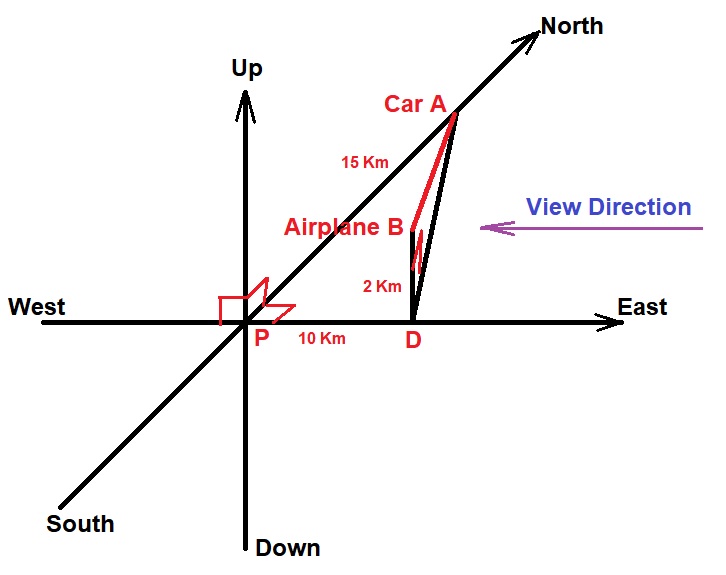
Please note the purple arrow showing the direction of our view as we look at the right triangle `Delta ABD`. That view is shown below:

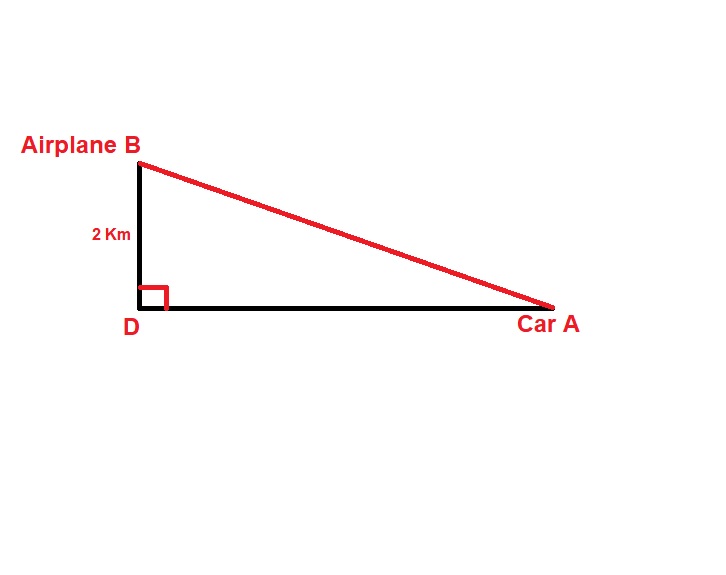
From the top picture, we can see that `Delta APD` is a right triangle. We can use the Pythagoras' formula to calculate the distance `AD`:

`(AD)^2=(AP)^2+(PD)^2` `color(red)(Equation 1)`

`(AD)^2=15^2+10^2=225+100=325`

`AD=sqrt325` `Km`

Now, we can use the lower picture and calculate the distance `AB` which is the distance between the Car and the Airplane at the moment described in the problem:

`(AB)^2=(AD)^2+(BD)^2` `color(red)(Equation 2)`

`(AB)^2=325+4=329`

`AB=sqrt329` `Km`

Let's plug the right hand side of equation 1 into equation 2 to substitute for `(AD)^2`:

`(AB)^2=(AP)^2+(PD)^2+(BD)^2`

For simplicity, let's let:

`AB=l`

`AP=y`

`PD=x`

`BD=z`

Then our equation becomes:

`l^2=y^2+x^2+z^2`

We need to find the rate of change of distance `l` at the moment specified in the problem. As such, we will take the derivative of the entire equation (both sides) with respect to time `t`:

`2l(dl)/dt=2y(dy)/dt+2x(dx)/dt+2z(dz)/dt`

We know that, at the specified moment, the car is traveling at `60` `Km`/`hr` and is `15` `Km` north of point `P`. Therefore:

`y=15` and `dy/dt=60`

The airplane is traveling at `190` `Km`/`hr` and is `10` `Km` east of point `P`. Therefore:

`x=10` and `dx/dt=190`

The airplane is `2` `Km` above the ground and that altitude is constant. Therefore:

`z=2` and `(dz)/dt=0`

Now, let's plug in known values at the specified moment:

`2(sqrt329)(dl)/dt=2(15)(60)+2(10)(190)+2(2)(0)`

`2sqrt329(dl)/dt=1800+3800+0=5600`

`(dl)/dt=5600/(2sqrt329)=154.37` `Km`/`hr`

At the specified moment, the distance between the car and the airplane is changing at the rate of `154.37` `Km`/`hr`.