Question

How to calculate the largest area of a rectangle inscribed in a circle with a radius of 13?

Answer 1

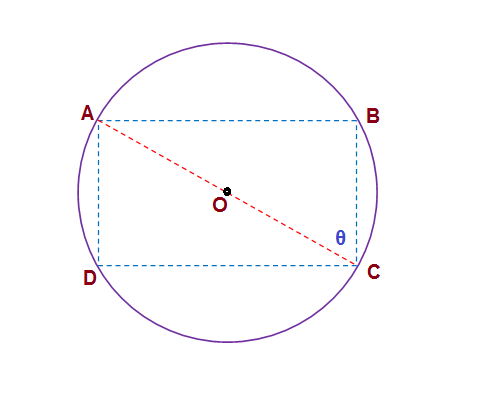
Let us consider that `ABCD` is the rectangle inscribed in a circle of radius `13` unit. As semicircular angle is right angle, diagonal `AC` will be the diameter of the circle. So `AC=26` unit.

Now let the `angleACB=theta`

So side `BC=ACcostheta` and side `AB=ACsintheta`

Now area `(S)`of the inscribed rectangle will be given by
`S=ABxxBC=ACsinthetaxxACcostheta=AC^2sinthetacostheta`

`=>S=26^2sintheta costheta=2xx13^2sin2theta`

Now area `S` will be maximum when `sin2theta` becomes maximum i.e `sin2theta=1=>theta=45^@`

Hence maximum area `S_"max"=2xx13^2=338` squnit

As `theta=45^@`, the rectangle becomes a square which is treated as a special kind of rectangle.