A circle passes through the point (-2,1) and touches the straight line 3x-2y=6 at the point (4,3).find its equation?
1 Answer
The equation is:
Explanation:
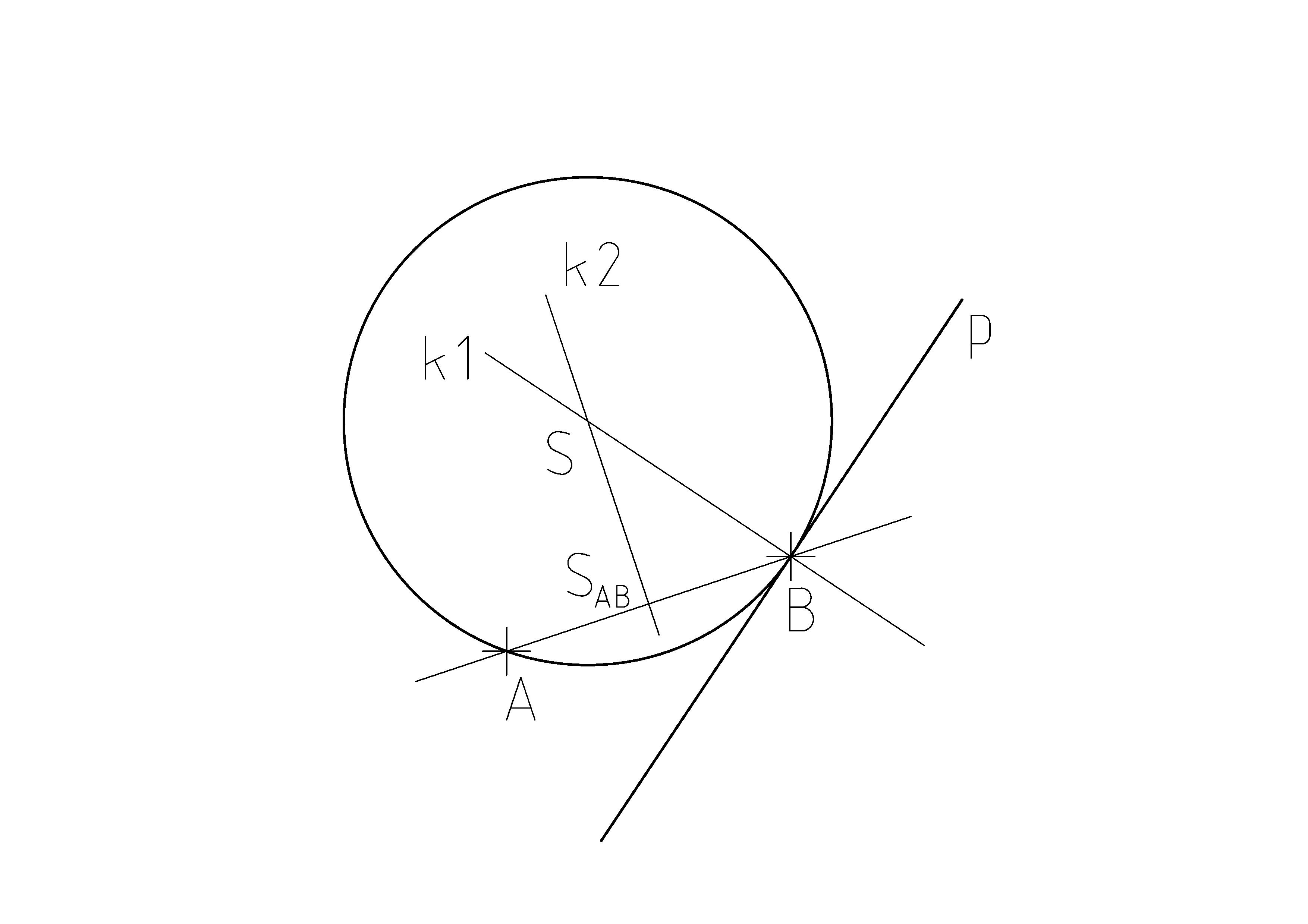
From your equation: normal vector of p:
You need to find point
Now you need to find the intersection of of k1 and k2. If (3,-2) is normal vec of p, than it is also directional vec of k1.
Similarly we can find vec of k2.
Direct. vec of AB is B-A -> (6,2). Normal vec of AB is than (2,-6) which is also direct. vec of k2.
Now we can build parametric equations of k1 and k2:
k1:
k2:
We put
We will get
Fit
The penultimate step: radius
General circle equation:
After fitting:

