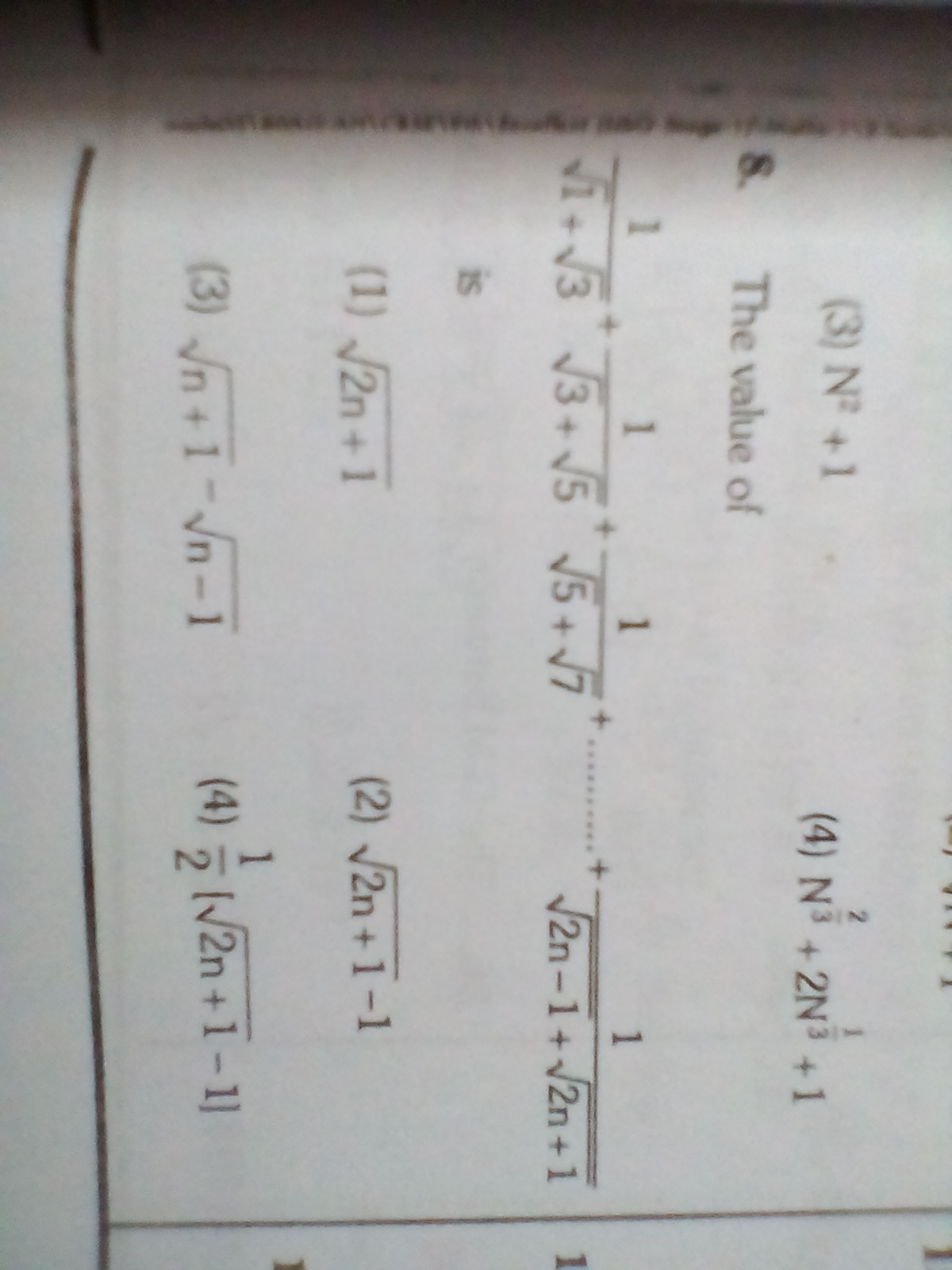General term, #T_n = 1/( (2n-1)^(1/2)+(2n+1)^(1/2))#
Rationalize the General term of the sequence :-
#rArr T_n = ( (2n-1)^(1/2)-(2n+1)^(1/2))
/[( (2n-1)^(1/2)+(2n+1)^(1/2)).( (2n-1)^(1/2)-(2n+1)^(1/2))]#
#rArr T_n = ((2n-1)^(1/2)-(2n+1)^(1/2))/(-2)#
#rArr T_n = ((2n+1)^(1/2)-(2n-1)^(1/2))/2#
Now summing all the terms ie.
#rArr sum T_n = sum_(n=0)^n((2n+1)^(1/2)-(2n-1)^(1/2))/2#
#rArr sum T_n = [(3-1)+(5-3)+.............+((2n+1)^(1/2)-(2n-1)^(1/2))]/2#
#rArr sum T_n = [(cancel3-1)+(cancel5-cancel3)+.............+((2n+1)^(1/2)-cancel(2n-1)^(1/2))]/2#...........................#($)#
#:. sum T_n = [(2n+1)^(1/2)-1]/2#....................option #(4)#
#NOTE# :- In equation #($)# we should note a Pattern of
cancellation of the terms has formed ; where the initial
terms are eliminated by the succeeding terms at some point ,
except the Least and the Biggest terms which are #1# and
#(2n+1)^(1/2)# respectively and the term #(2n-1)^(1/2)# also gets
cancelled.