Given the formula for the area of a square is:
#A = s^2# where #A# is the Area and #s# is the length of the side of the square, we can find the length of one side of the square by substituting and solving:
#9" in"^2 = s^2#
#sqrt(9" in"^2) = sqrt(s^2)#
#3" in" = s#
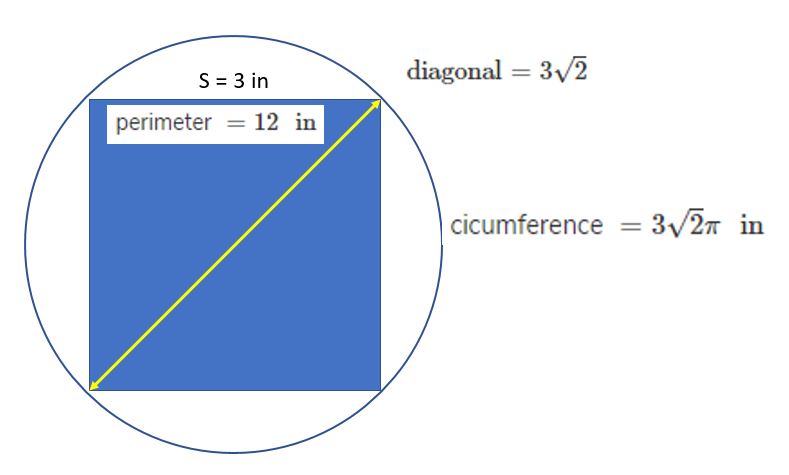
#s = 3" in"#
Using the Pythagorean Theorem we can find the length of the squares diagonal which is also the diameter of the circle:
The Pythagorean Theorem states:
#a^2 + b^ = c^2# where #a# and #b# are legs of the triangle and #c# is the hypotenuse of the right triangle. In this case, both legs of the triangle are sides of the square so the are both the same length. Substituting and solving gives:
#(3"i n")^2 + (3"i n")^2 = c^2#
#9" in"^2 + 9" in"^2 = c^2#
#9" in"^2 xx 2 = c^2#
#sqrt(9" in"^2 xx 2) = sqrt(c^2)#
#sqrt(9" in"^2)sqrt(2)" in" = c#
#3" in"sqrt(2) = c#
#c = 3sqrt(2)" in"#
We can now find the perimeter of the square and the circumference of the circle.
Formula for Perimeter of a square is:
#p = 4s# where #s# is the length of a side of the square.
Substituting and calculating #p# gives:
#p = 4 xx 3" in"#
#p = 12" in"#
Formula for the circumference of a circle is:
#c = 2pir# where #r# is the radius of the circle.
Or,
#c = dpi# where #d# is the diameter of the circle. Remember: #d = 2r#
Substituting and calculating #c# gives:
#c = 3sqrt(2)pi" in"#
We can then write the ratio of the circumference to perimeter as:
#(3sqrt(2)pi" in")/(12" in") =>#
#(color(blue)(cancel(color(black)(3)))sqrt(2)picolor(red)(cancel(color(black)(" in"))))/(color(blue)(cancel(color(black)(12)))4color(red)(cancel(color(black)(" in")))) =>#
#(sqrt(2)pi)/4#

