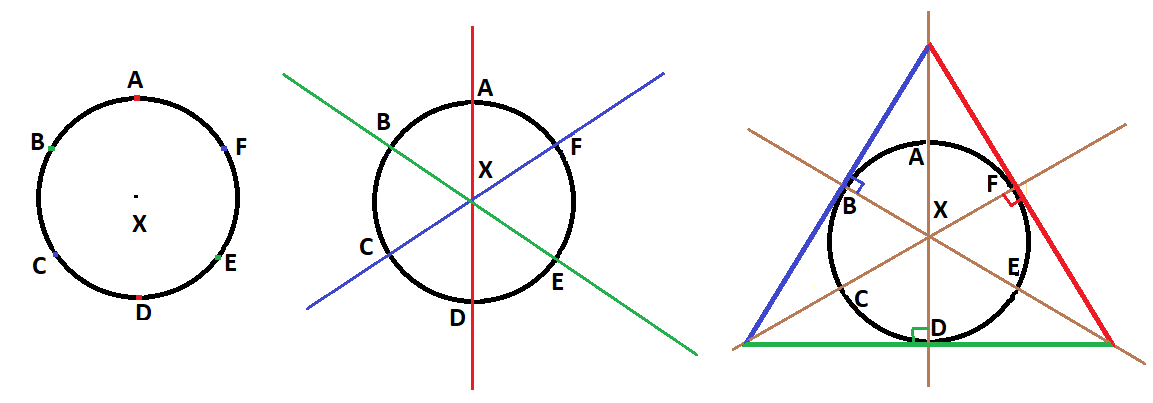
Question #3e595
1 Answer
Use the standard Euclidean construction tools.
Explanation:
I assume you are either given or can construct the circles with the given radii.
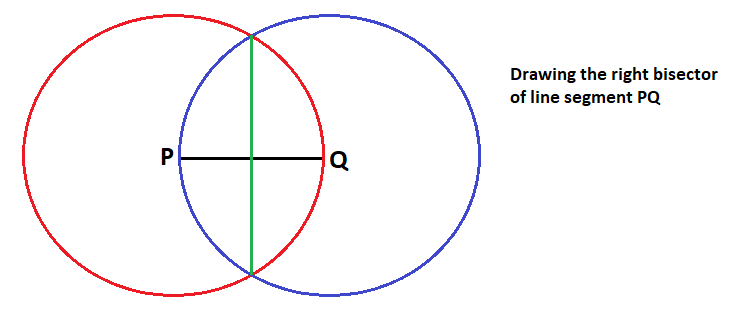
An essential tool is the ability to construct a perpendicular ("right") bisector of a line segment.
Given a line segment
with center
with center
* connect the two points where the circles intersect to form the right bisector.
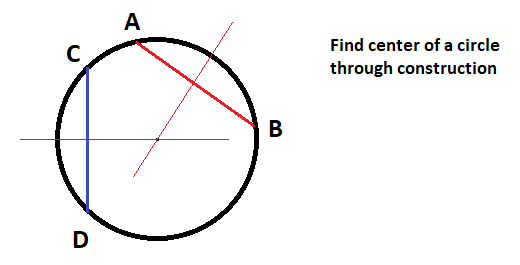
For any of the given circles:
draw any two distinct cords
draw the right bisector for each cord
* the point where the bisector lines intersect will be the center of the circle.
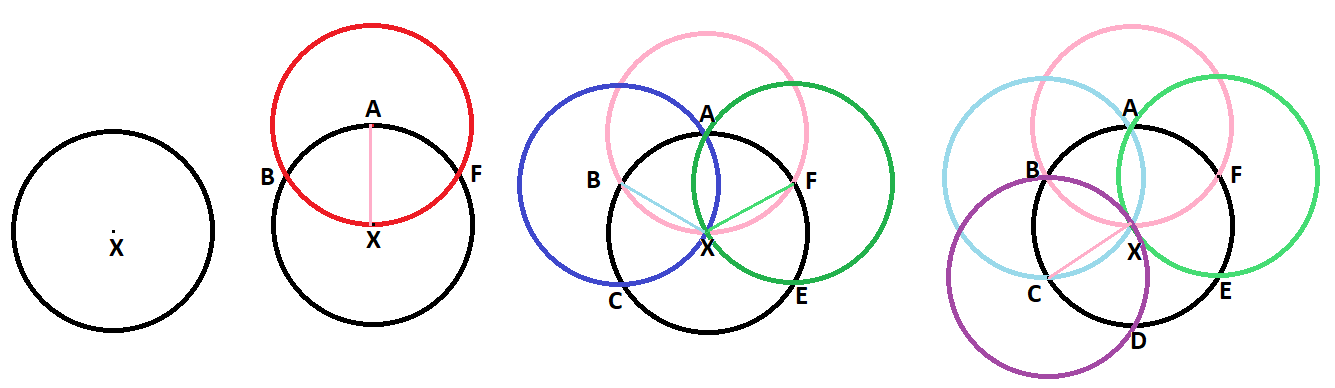
For the given circle (and determined center
subdivide the circle into 6 equal arcs:
pick an arbitrary point
with center
label the points where the new circle intersects the given circle as
repeat this process using points
* repeat this process one more time with center
The points
Using the arc end points
draw (extended) lines through pairs of points on opposite sides of the given circle; that is through
draw lines perpendicular to those just constructed through the alternate points
These three new lines will intersect to form an equilateral, circumscribing triangle.