Solve for w . Simplify?
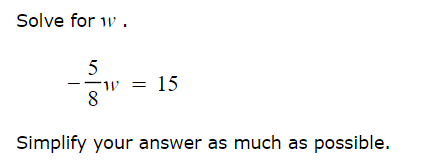
4 Answers
The value of
Explanation:
As long as you perform the same operations on both sides of the equation, you can do whatever you want. First, multiply both sides by
Explanation:
Step 1
The first priority is to isolate the variable
Step 2
In order to simplify the left side of the equation, we can simply cancel the
Step 3
Now, we must simplify the right side of the equation. When dividing by a fraction, we can simply multiply by the fraction's reciprocal.
Step 4
We simplify.
Explanation:
1) Clear the fraction by multiplying both sides by
2) Divide both sides by
Answer:
Explanation:
We have:
Using the fact that
=>
Now, remember that:
If
=>
=>
=>
=>




