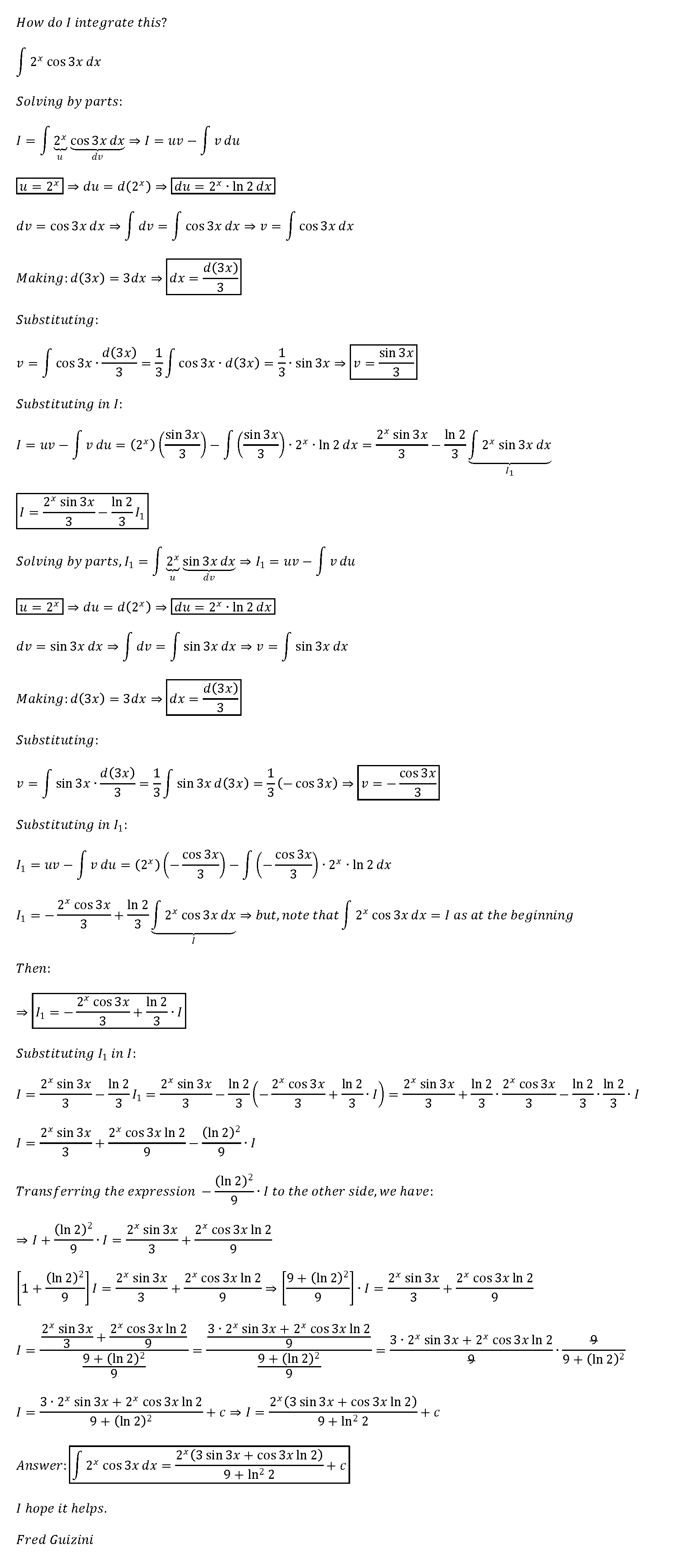How do i integrate this?
2^(x)*cos3x dx
2^(x)*cos3x dx
2 Answers
I=(e^(ln(2)x)(3sin(3x)+ln(2)cos(3x)))/((ln(2))^2+3^2)+C
Explanation:
We want to solve
I=int2^xcos(3x)dx=inte^(ln(2)x)cos(3x)dx
Lets try the more general problem
I_1=inte^(ax)cos(bx)dx
Where we seek the solution
I_1=(e^(ax)(bsin(bx)+acos(bx)))/(a^2+b^2)+C
The trick is to use integration by parts twice
intudv=uv-intvdu
Let
Then
I_1=1/be^(ax)sin(bx)-a/binte^(ax)sin(bx)dx
Apply integration by parts to the remaining integral
I_2=a/binte^(ax)sin(bx)dx
Let
Then
I_2=a/b(-1/be^(ax)cos(bx)+a/binte^(ax)cos(bx)dx)
=-a/b^2e^(ax)cos(bx)+a^2/b^2inte^(ax)cos(bx)dx
=-a/b^2e^(ax)cos(bx)+a^2/b^2I_1
Substitute this into the original integral and solve for
it's a bit long, but we take it step by step
I_1=1/be^(ax)sin(bx)-(-a/b^2e^(ax)cos(bx)+a^2/b^2I_1)
I_1=1/be^(ax)sin(bx)+a/b^2e^(ax)cos(bx)-a^2/b^2I_1
I_1+a^2/b^2I_1=1/be^(ax)sin(bx)+a/b^2e^(ax)cos(bx)+C
(a^2+b^2)/b^2I_1=1/be^(ax)sin(bx)+a/b^2e^(ax)cos(bx)+C
I_1=b^2/(a^2+b^2)(1/be^(ax)sin(bx)+a/b^2e^(ax)cos(bx))+C
I_1=1/(a^2+b^2)(be^(ax)sin(bx)+ae^(ax)cos(bx))+C
I_1=(e^(ax)(bsin(bx)+acos(bx)))/(a^2+b^2)+C
For your problem
I=(e^(ln(2)x)(3sin(3x)+ln(2)cos(3x)))/((ln(2))^2+9)+C
Hopefully there aren't to many mistakes
See the answer below: we have solved using discrete elements instead of a general formulation and we did not simplify the final result, as follows: