Can someone explain why this happens?
Say we have a function of #x# , for example #y=x^(1/2)# , we can also write this as #x=y^2#
By taking the derivative of #y=x^(1/2)# , we get #y'=x^(-1/2)/2#
By implicity differenciating #y^2=x# we get #y'=1/(2y)#
If we make #1/(2y)=x^(-1/2)/2# and rearrange to make #y# the subject, we get #y=x^(1/2)# , which was the original function.
However, for other functions, i.e. #y=sqrt(arcsin(x))# the function for equating both differentials gives a graph which include #y=sqrt(arcsin(x))# along with some other stuff.
Say we have a function of
By taking the derivative of
By implicity differenciating
If we make
However, for other functions, i.e.
2 Answers
You should get the same graph as the original function.
Explanation:
If
#{dy}/{dx} = 1/(2sqrt((1-x^2)arcsin(x)))#
On the other hand, we can write the first equation as
#x = sin(y^2)#
Differentiating implicitly gives
#1 = cos(y^2) (2y) {dy}/{dx}#
or
#{dy}/{dx} = 1/(2ycos(y^2))#
If you want to equate the 2 "different"
#1/(2sqrt((1-x^2)arcsin(x))) = 1/(2ycos(y^2))#
Simplifying it gives
#(1-x^2)arcsin(x) = y^2cos^2(y^2)#
which seem complicated but notice that the original equation
I think I understand.
Explanation:
If I graph
I get:
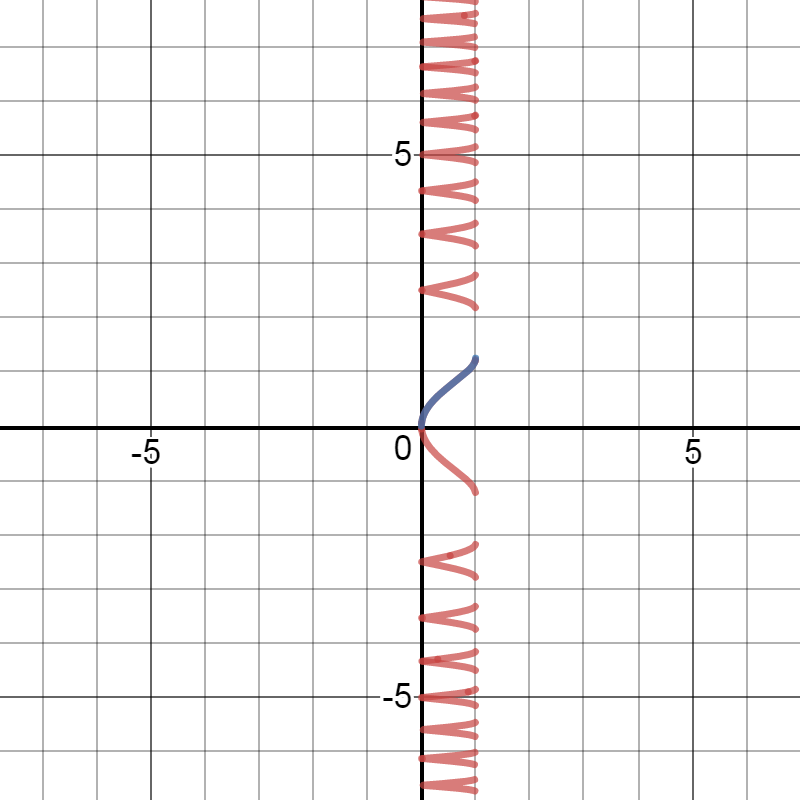
The little blue piece is
For
There is no such restriction on the


