Question

Benhur is standing `200` feet from the base of a tall building. If he determines that the angle of elevation from the ground to the top of the building is `50` degrees, how tall is the building?

Answer 1

`238.4` feet high

Explanation:

The question describes a right-angled triangle (We assume the building is vertical and the ground is horizontal giving an angle of `90°`

The angle of `50°` where Benhur is standing is the angle between the ground and the line to the top of the building.

The distance of `200` feet is the adjacent side and the height of the building is the opposite side, `x,` which we need to find.

Therefore we can use the Tan ratio.

`x/200 =tan50`

`x = 200 xx tan 50`

`x = 238.4` feet

Answer 2

The building is `238.4\ ft` tall.

Explanation:

``
``
``
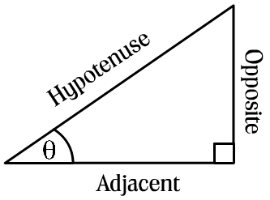
In a right triangle, the hypotenuse is the longest side, an "opposite" side is the one across from a given angle, and an "adjacent" side is next to a given angle.
``
``
For acute angle `\theta` in a right triangle, the trigonometric ratio's are:

`sin(\theta )=\frac{\text{Opposite}}{\text{Hypotenuse}}`
`cos(\theta )=\frac{\text{Adjacent}}{\text{Hypotenuse}}`
`tan(\theta )=\frac{\text{Opposite}}{\text{Adjacent}}`

``
``
``
We are given with:

`\text{Adjacent}=200\ ft` `\ \ \ \`and`\ \ \ \` `\theta = 50^{\circ}`
Let's say the required height of the building is `x` feets, which represents the `Opposite`.

By applying the trigonometric ratio of `tan`, we can find the value of `x`.

`tan(50^{\circ })=\frac{x}{200}`

Multiply both sides by 200, switch sides and then simplify to get:

`x=238.4\ ft`