Find a vector function, #r(t)#, that represents the curve of intersection of the two surfaces. The cylinder #x^2 + y^2 = 81# and the surface #z = xy#?
2 Answers
The curve of intersection may be parametrized as
Explanation:
I am not sure what you mean by vector function. But I understand it that you seek to represent the curve of intersection between the two surfaces in the question statement.
Since the cylinder is symmetric around the
Change to cylindrical coordinates:
Then the first surface becomes
because of the Pythagorean trigonometric identity.
The second surface becomes
We learned from the equation of the first surface that the intersecting curve must be at a squared distance
a curve parametrized by
From this expression we see that the curve is indeed a curve, as it has one degree of freedom.
All, in all, we can write the curve as
which is a vector valued function of a single variable
See below.
Explanation:
Considering the intersection of
with
or
we have
now solving for
which are real for
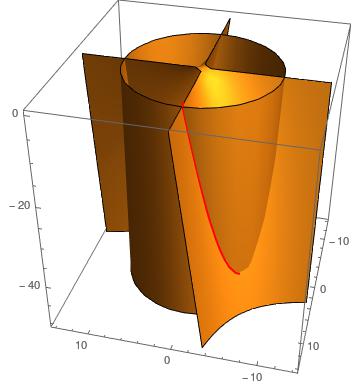
Attached a plot showing the intersection curve in red (one leaf).