Question

A cone has a height of `24 cm` and its base has a radius of `15 cm`. If the cone is horizontally cut into two segments `12 cm` from the base, what would the surface area of the bottom segment be?

Answer 1

22.1 SQ CM

Explanation:

Requires reworking based on the details given below

`A_T= A_B + A_b + L_R - L_r`

Where `A_T` is Total Surface Area of the bottom truncated cone, `A_B` is the area of the bottom circular base, `A_b` is the area of the circular base of top cut cone, `L_R` is the Lateral Surface Area of the whole cone and `l_r` is the Lateral Surface Area of the top half cone.

Answer 2

Total Surface Area of the bottom segment of the cone

`A_(R-r) = color(purple)(1882.6)cm^3`

Explanation:

`r / R = h / H`

`r = (15 * (24-12))/24 = 7.5 cm`

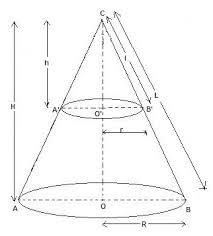
Lateral surface are of a cone `L_R= pi R L`

Now we have to find L

`L = sqrt(R^2 + H^2) = sqrt(15^2 + 24^2) ~~ 28.3 cm`

`L_R = pi * 15 * 28.3 ~~ 1333.6 cm^2`

Similarly,`l = sqrt(12^2 + 7.5^2) ~~ 14.2 cm`

`l_r = pi r l = pi * 7.5 * 14.2 ~~ 334.6`

Area of base of a cylinder `A_R = pi R^2 = pi * 15^2 ~~ 706.9`

Similarly, `A_r = pi r^2 = pi * 7.5^2 ~~ 176.7`

Total surface area of the truncated cone

`A_(R-r) = L_R - l_r + A_R + A_r = 1333.6 - 334.6 + 706.9 + 176.7 = color(purple)(1882.6)cm^3`