Question

How do you find the values of all six trigonometric functions of a right triangle ABC where C is the right angle, given a=20, b=21, c=29?

Answer 1

`cosB=a/c=21/29`

`sinB=b/c=20/29`

`tanB=b/a=20/21`

`cotB=a/b=21/20`

`secB=c/a=29/21`

`cscB=c/b=29/20`

Explanation:

Verification:

`20^2=400`
`21^2=441`
`20^2+21^2=400+441`
`20^2+21^2=841`
`29^2=841`
It is confirmed that the triangle is a right angled triangle
`a=20`
`b=21`
`c=29`
`C=90^@`
Thus with c=29 being considered as hypotenuse
Consider a=21 to form the adjacent side
, and b=20 to form the opposite side
the angle under consideration is B

Now,

`cosB=a/c=21/29`

`sinB=b/c=20/29`

`tanB=b/a=20/21`

`cotB=a/b=21/20`

`secB=c/a=29/21`

`cscB=c/b=29/20`

Answer 2

all trignometric functions of right triangle, AC= hypotenuse=c
BC=a and AC= b are adjacent or opposite sides in accordance to the acute angles, either A or B

Explanation:

if we take angle A as the acute angle,
`sinA= a/c=20/29=(opp)/(hyp)`
`cosA=b/c=21/29=(adj)/(hyp)`
`secA=c/b=29/21=(hyp)/(adj)`
`cosecA=c/a=29/20=(hyp)/(opp)`
`tanA=a/b=20/21=(opp)/(adj)`
`cotA= b/a=21/20=(adj)/(opp)`

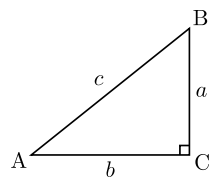
if we take angle B as the acute angle,
`sinB= b/c=21/29=(opp)/(hyp)`
`cosB=a/c=20/29=(adj)/(hyp)`
`secB=c/a=29/20=(hyp)/(adj)`
`cosecB=c/b=29/21=(hyp)/(opp)`
`tanB=b/a=21/20=(opp)/(adj)`
`cotB= a/b=20/21=(adj)/(opp)`