The equation for the photoelectric effect is
color(blue)(bar(ul(|color(white)(a/a)hf = Φ + KEcolor(white)(a/a)|)))" "
where
h color(white)(ml)= Planck's constant
f color(white)(ml)= the frequency of the incident light
Phicolor(white)(m) = the work function
KE = the kinetic energy of the ejected electron
We can rearrange the equation to get
KE = hf - Phi
Compare this equation with that for a straight line.
KE = hf - Phi
color(white)(ll)ycolor(white)(ll) = mx + b
Thus, a plot of KE vs f is a straight line with slope h" and x- intercept Phi.
I converted the wavelengths to frequencies and got the following dataset.
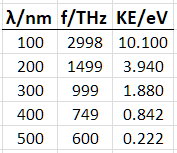 Data
Data
The plot of KE vs f looked like this.
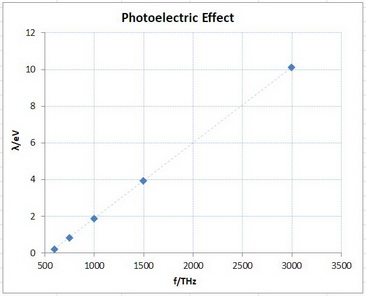 Graph
Graph
The calculated equation for the line is KE = "0.004 118"f- 2.240
The y-intercept is at
"0 = "0.004 118"f- 2.2404
f = 2.2404/"0.004 118" = "544 THz"
"slope" = h =("0.004 118" color(red)(cancel(color(black)("eV"))))/(1 color(red)(cancel(color(black)("THz")))) ×(1.602 × 10^"-19" color(white)(l)"J")/(1 color(red)(cancel(color(black)("eV")))) × (1 color(red)(cancel(color(black)("THz"))))/(10^12color(white)(l) "s"^"-1") =
6.597 × 10^"-34"color(white)(l) "J·s"
The experimental value for h = 6.597 × 10^"-34"color(white)(l) "J·s".
The work function corresponds to the point where the excess kinetic energy of the electron is zero.
0 = hf - Phi
Phi = hf = 6.626 × 10^"-34"color(white)(l) "J·"color(red)(cancel(color(black)("s"))) × 544 × 10^12 color(red)(cancel(color(black)("s"^"-1"))) = 3.60 × 10^"-19"color(white)(l) "J"
In electron volts, the work function is
Phi = 3.60 × 10^"-19" color(red)(cancel(color(black)("J"))) × "1 eV"/(1.602 × 10^"-19" color(red)(cancel(color(black)("J")))) = "2.25 eV"

 Data
Data  Graph
Graph 
