Question

A 25 foot building casts a 6 foot shadow. How tall is the building that casts a 24 foot shadow at the same tiene?

Answer 1

The building that casts a `24` foot shadow at the same time is `10` feet tall.

Explanation:

Let's make a sketch of the first building, using a right triangle. The vertical height of our triangle will be the `25` foot building, while the horizontal base will be the `6` foot cast shadow:

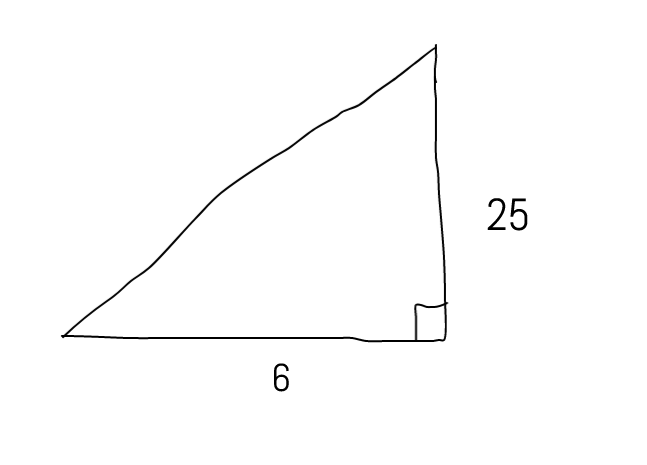
Now, we need a sketch of the building that casts a `24` foot shadow at the same time. Since these shadows are being cast at the same time, let's draw the second sketch in such a way that the first sketch is inside of it. For this building, we'll denote the unknown height by `h`.

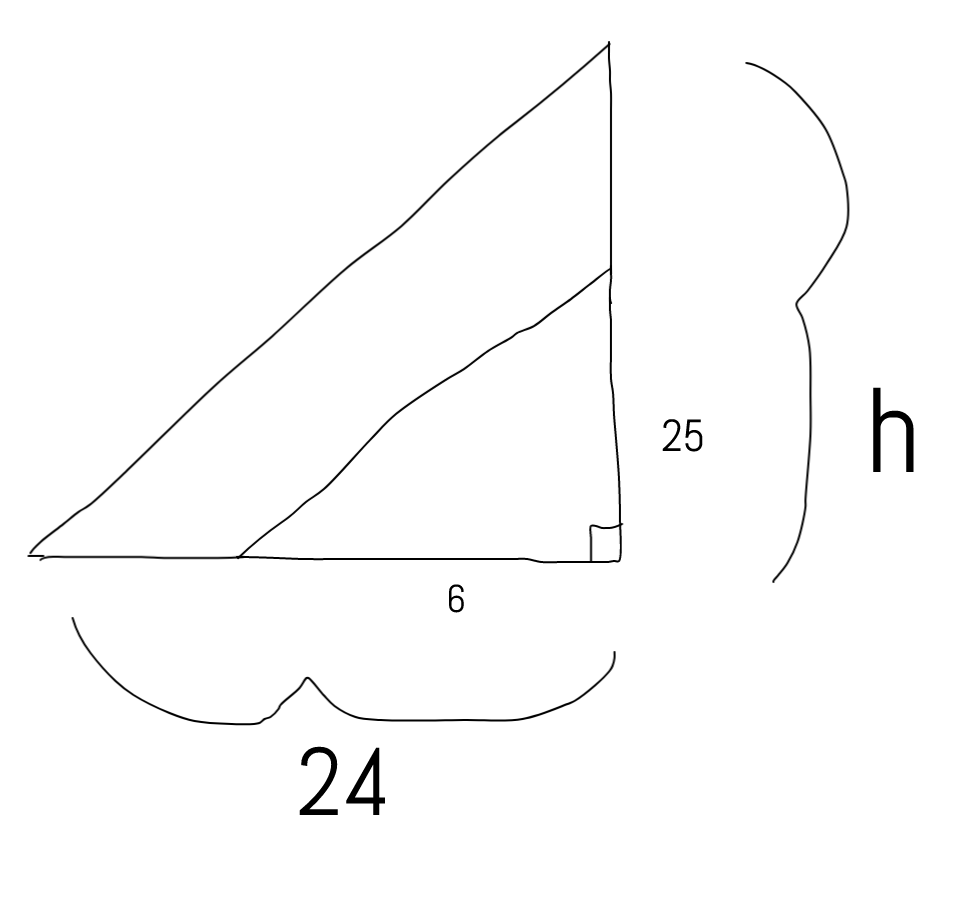
We now have two right triangles that we can call similar . This means that their corresponding angles are congruent and therefore their sides are proportionate (we can say they are similar because a) they're both right triangles and b) we're discussing two vertical buildings casting shadows at the same time, there's no indication that anything changes shape-wise or angle-wise between the two scenarios).

Knowing that the sides of the triangles are proportionate means that we can say

`h/25=24/6`

In other words, the vertical height of the larger triangle divided by the vertical height of the smaller triangle is equal to the horizontal base of the larger triangle divided by the horizontal base of the smaller triangle.

Solving for `h:`

`(h(cancel25)/cancel25)=(24(25))/6`
`h=600/6=10`

The building that casts a `24` foot shadow at the same time is `10` feet tall.