First, we want everything in this equation to be in the form of one trigonometric function. Let's have everything in the form of cos(x).
Recall the following identity:
sin(2x)=2sin(x)cos(x)
Rewrite with this applied:
cos(2x)cos(x)+2sin(x)cos(x)sin(x)=1
cos(2x)cos(x)+2cos(x)sin^2(x)=1
Recall that
sin^2(x)+cos^2(x)=1
Solving for sin^2(x) gives
sin^2(x)=1-cos^2(x)
Apply this to the instance of sin^2(x) in the equation:
cos(2x)cos(x)+2cos(x)(1-cos^2(x))=1
Distribute 2cos(x) through:
cos(2x)cos(x)+2cos(x)-2cos^3(x)=1
Recall the following identity:
cos(2x)=2cos^2(x)-1 (There are three ways to write the double-angle identity for cos(2x); however, we only want the one where everything is in terms of cos(x))
Apply:
(2cos^2(x)-1)cos(x)+2cos(x)-2cos^3(x)=1
Multiply cos(x) through and simplify:
cancel(2cos^3(x))-cos(x)+2cos(x)-cancel(2cos^3(x))=1
Now, we have a very simple equation to solve:
cos(x)=1
We want all values of x for which cos(x)=1.
cos(x)=1 for x=2pin where n is any integer. We must include n because the period of cos(x) is 2pi, meaning that any value of cos(x) repeats every 2pi units (regardless of whether we add or subtract 2pi). cos(0)=1, but so does cos(2pi), cos(4pi), cos(-2pi), and infinitely many other values obtained; therefore, we account for these with 2pin.
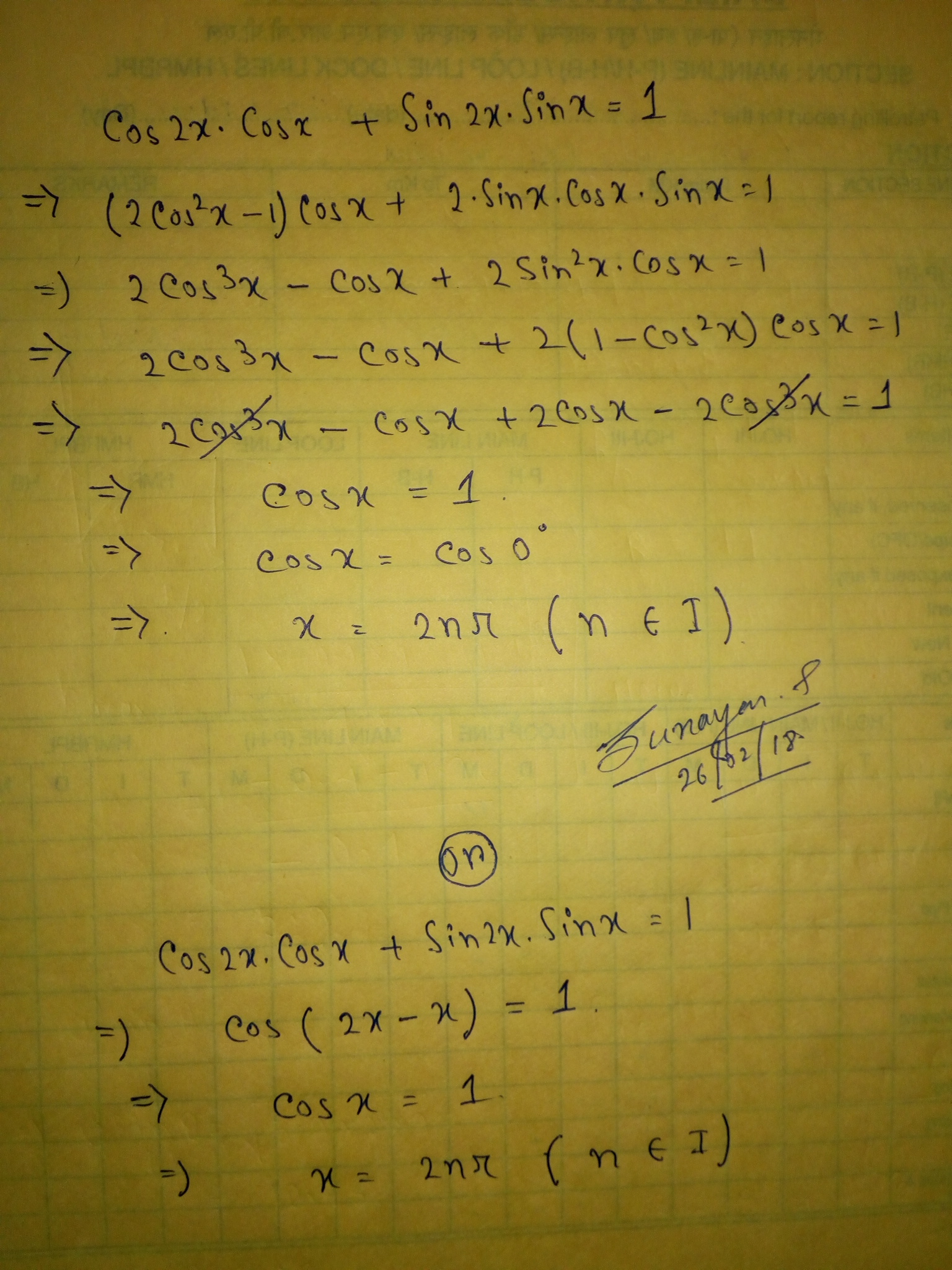 My notebook...
My notebook... 

