Question #fd431
1 Answer
Explanation:
If you don't immediately know what to do, ALWAYS draw a diagram.
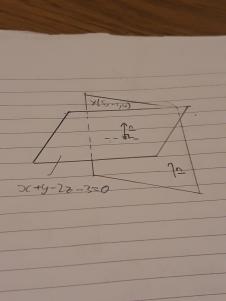
Here, I have the plan given, and the one intercepting it. I've marked a normal vector to the plane given,
If the two planes are perpendicular, then the normal vector to one plane will be a vector parallel to the other plane. Also, the normal vector to each plane will be perpendicular to each other, and dot product to zero.
Let
To find a vector perpendicular to this one:
Let
Let
There are no unique solutions to this, so let's find a perpendicular vector.
Let
Let
To check this is normal to the desired plane,
Since we now have a vector normal to our desired product, we can use the scalar product equation of a plane:
In Cartesian form:
