#color(blue)("Considering initial condition")#
The absolute type brackets are still just brackets. Special ones admittedly. They state the any calculation that occurs inside is to be interpreted as ending up as positive
Example #|-2|=|+2|=+2#
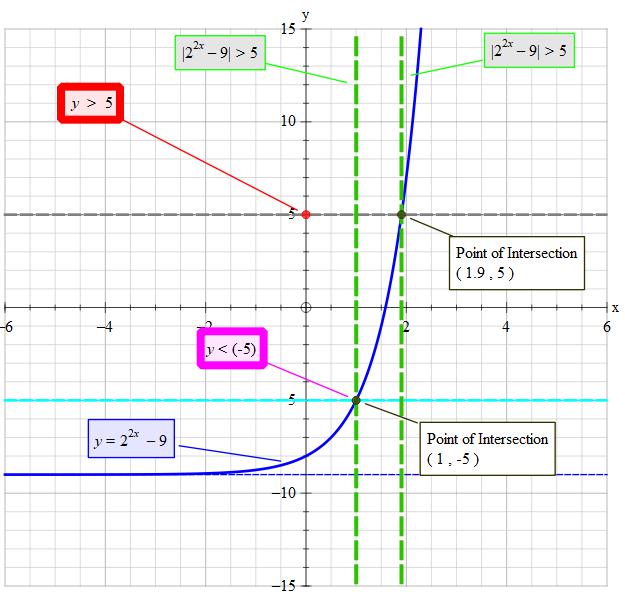
So if we set #y=|2^(2x)-9|# we can only accept the value of #x# that give #y>5#
So if the content of the absolute is set at #b# we can only accept
#|color(white)(./.)+5 < b < -5color(white)(./.)|#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determining the critical point 1")#
Set the critical point 1 as #P_1->y_("critical")=-5=2^(2x)-9#
#-5+9=2^(2x)#
#4=2^(2x)#
We know that #2^2=4# so
#2^(2x) =2^2# thus #x=1#
As #x# becomes less then #2^(2x)# becomes less. Also #2^(2x)-9# becomes more negative. So we have #x<1#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determining the critical point 2")#
Set the critical point 2 as #P_2->y_("critical")=+5=2^(2x)-9#
#14<2^(2x)#
#ln(14)<2xln(2)#
#x> ln(14)/(2ln(2))#
#x~~1.903677.......#
#x~~1.90# to 2 decimal places #larr" Reasonable answer"#
#2^(2xx1.90) ~~13.928...#
#2^(2xx1.91)~~14.123...#
As #x# gets greater than #1.91" then "{2^(2xxx)-9}# becomes greater than +5
So we have #x>1.90# to 2 decimal places
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Putting it all together")#
#1 >x >1.90# approximately
#1>x>ln(14)/(2ln(2))# exactly
#color(magenta)("Graph showing how it all ties together")#